Выражения со скобками
Приоритет операций
Какое значение имеет следующее выражение?
3+2∙4
Как считать? Сложить 3 и 2, получив 5, а потом умножить 5 на 4, тогда получится 20? Или сначала умножить, получив 8, затем прибавить 3 и получить 11?
Конечно же, больший приоритет имеет умножение и деление, и только потом сложение и вычитание. Поэтому вышеописанное выражение имеет значение 11:
3+2∙4=3+8=11
То же касается и деления – приоритет деления выше приоритетов сложения и вычитания:
3+4∶2=3+2=5
3−4∶2=3−2=1
В том случае, когда нам нужно все-таки сначала сложить два числа, а потом умножить полученный результат, то применяются скобки – они имеют наибольший приоритет:
(3+2)∙4=5∙4=20
Раскрытие скобок
Очень часто приходится выражение со скобками заменять равносильным ему без скобок. Попробуем избавиться от скобок в таком выражении, не складывая 3 и 5:
2∙(3+5)
Что значит умножить число 3+5 на 2? Это значит: увеличить его в два раза. Но обязательно ли для того, чтоб удвоить 3+5, предварительно складывать эти числа? Можно удвоить сначала 3, потом 5 и сложить результат:
2∙(3+5)=2∙3+2∙5
Следующий рисунок делает очевидным ответ на вопрос, почему два раза по восемь кругов равны двум разам по три и двум разам по пять кругов.
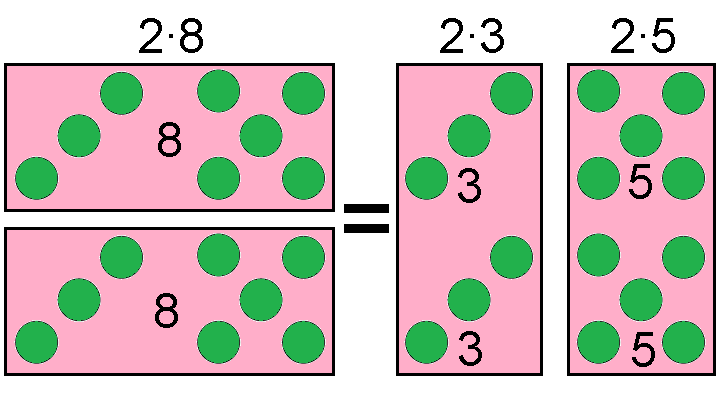
Проверим равносильность обоих выражений:
2∙(3+5)=2∙8=16
2∙3+2∙5=6+10=16
Как видно, оба выражения имеют значение 16 – значит, они равносильны и между ними можно поставить знак равно:
2∙(3+5)=2∙3+2∙5
Возьмем, к примеру, такое выражение:
2∙(x+5)
Здесь вместо удобного числа 3 оказалась переменная x, и сколько будет x+5 посчитать уже не удастся. Число x – это самое обычное число, просто оно не известно, и к нему можно применить тот же самый метод: домножить каждое слагаемое в скобке на 2:
2∙(x+5)=2∙x+2∙5
Знак равенства между этими выражениями означает, что первое выражение со скобками абсолютно равносильно второму, в котором нет скобок. Значит, можно вместо x подставить совершенно любое число в оба выражения и получить одно и то же значение. Например, подставим вместо x число 7 в выражение со скобками:
2∙(7+5)=2∙12=24
Получилось 24, а теперь подставим вместо x число 7 в выражение без скобок:
2∙7+2∙5=14+10=24
Попробуйте подставить любое другое число вместо x и оба выражения дадут совершенно одинаковый результат.
Умножая каждое число в скобках на число за скобками, следует учитывать какой знак стоит перед этими числами – "плюс" или "минус". Если перед числом нет ни плюса, ни минуса, значит, там стоит плюс, просто его не пишут. В следующем примере перед числом 8 и числом 11 нет знака (значит, считаем, что перед ними стоит плюс), а плюс на плюс – дает плюс, значит, и перед 8∙11 будет плюс, который там тоже не написан, но подразумевается. А вот перед числом 3 – знак "минус", а минус на плюс – дает минус, следовательно, перед 3∙11 будет стоять минус:
(8−3)∙11=8∙11−3∙11
(41−37)∙23=23∙41−23∙37
Слагаемых внутри скобок может быть сколько угодно, но суть метода от этого не меняется, чтобы раскрыть следующую скобку, нужно таким же образом умножить каждое число в скобках на 2:
2∙(1+2+3+4)= 2∙1+2∙2+2∙3+2∙4
И еще пример с минусами:
4∙(14−3+19—4+1−2)=
=4∙14−4∙3+4∙19−4∙4 +4∙1−4∙2
Вынесение общего множителя за скобку
Необходимо уметь еще и производить обратную операцию – заменять выражение без скобок равносильным со скобками. Например, возьмем число 14 в таком виде:
6+8
Если уменьшить это число в два раза, разделив каждое слагаемое на два, а затем умножить его на два, но уже не по отдельности, а все число сразу, то число 14 не изменится, а скобка появится:
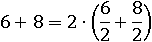
Для упрощения каждую дробь можно заменить равным ему числом:
6+8=2∙(3+4)
Такое действие называется вынесением общего множителя за скобку.
Аналогичным образом выносят общий множитель за скобку при наличии минусов и большого количества слагаемых: делят все числа на число, которое будет общим множителем, и после умножают на него же:
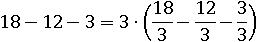
Легко проверить, что по обе стороны от знака равно одно и то же число 3:
18−12−3=3∙(6−4−1)=3
Умножение скобки на скобку
Бывает и так, что скобка умножается на скобку:
(8+3)∙(5+2)
Чтобы раскрыть эти скобки, не складывая числа внутри, надо этот случай свести к предыдущему (как и везде в математике). Число в первой скобке – это просто число и ничего больше, значит, как и в предыдущем случае можно просто домножить на первую скобку каждое из чисел во второй скобке:
(8+3)∙(5+2)=(8+3)∙5+(8+3)∙2
И затем раскрыть каждую из скобок:
(8+3)∙5+(8+3)∙2= 8∙5+3∙5+8∙2+3∙2
Значит, оба выражения должны быть равными:
(8+3)∙(5+2)= 8∙5+3∙5+8∙2+3∙2
Значение выражения со скобками равно 77:
(8+3)∙(5+2)=11∙7=77
И значение выражения без скобок равно 77:
8∙5+3∙5+8∙2+3∙2= 40+15+16+6=77
Попробуем повторить то же самое с переменными:
(a+b)∙(x+y)=
=(a+b)∙x+(a+b)∙y=
=a∙x+b∙x+a∙y+b∙y
Но чисел может оказаться и гораздо больше:
(a+b+c)∙(x+y)=
=(a+b+c)∙x+(a+b+c)∙y
=a∙x+b∙x+c∙x+a∙y+b∙y+c∙y
Уже прослеживается некая закономерность: каждое число из первой скобки умножается на каждое из второй. И теперь нет нужды в промежуточном действии со скобками: нужно просто взять первое число в первой скобке и по порядку умножать его на каждое из второй, затем взять второе число из первой скобки и умножать его на каждое из второй: и так до тех пор, пока не дойдем до умножения последнего числа из первой скобки на последнее число из второй:
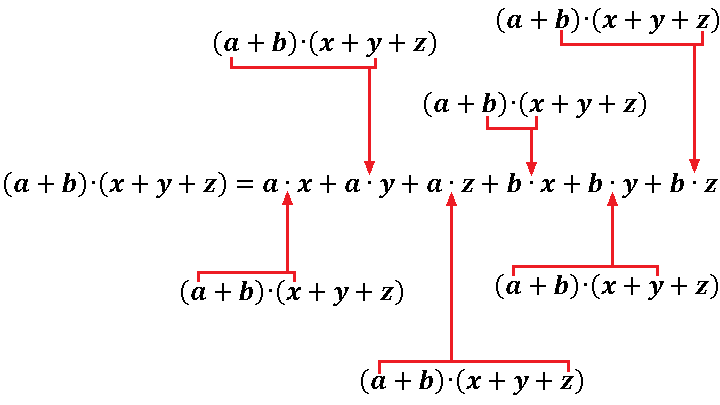
Попробуем новое правило в действии:
(3+7)∙(11+22)

И дальше
=3∙11+3∙22+7∙11+7∙22=
=33+66+77+154=330
И действительно, первая скобка, равная числу 10, при умножении на вторую скобку, равную числу 33 будет давать 10∙33=330.
Разумеется, следует понимать, что если в скобке перед b стоит минус, а перед y – плюс, то при умножении b на y перед b∙y будет минус, потому как плюс на минус дает минус. А если перед b и z — минусы, то когда b и z умножатся, перед b∙z будет плюс, так как минус на минус дает плюс:
(a−b)∙(x+y−z)=
=a∙x+a∙y−a∙z−b∙x−b∙y+b∙z
Подставим какие-нибудь числа и проверим:
(17−7)∙(18+3−1)=
=17∙18+17∙3−17∙1−7∙18−7∙3 +7∙1=
=306+51−17−126−21+7=200
Как видно, все сходится.
Дроби – такие же числа, и скобки с ними будут раскрываться, подчиняясь аналогичным правилам:
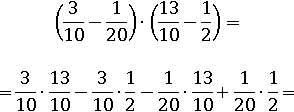
О том, как умножаются и складываются дроби, можно узнать тут, а пока продолжим:
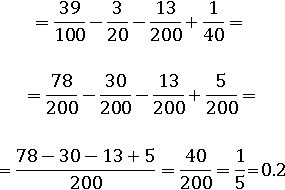
Проверить эти вычисления можно, сложив дроби в скобках, после чего умножить:
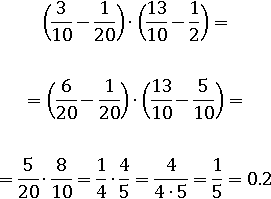
Второй способ проще, но нам надо было научиться раскрывать скобки, потому как далеко не всегда будет возможность сложить числа внутри скобок.