Основные арифметические операции с дробями
Дроби в математике будут всегда и везде, и с ними будут производиться самые разнообразные действия, поэтому нам для начала следует познакомиться с самыми базовыми из них.
Умножение дробей
Умножение является наиболее простой операцией, производимой с дробями.
Чтоб умножить одну дробь на другую, достаточно просто умножить числитель на числитель, а знаменатель на знаменатель:
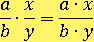
Например:
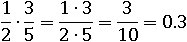
Проверим результат, умножив эти числа другим способом: одна вторая – это один, деленый на два. А один, деленый на два, равно 0.5:
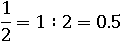
А три пятых – это три, деленое на пять, которое равно 0.6:
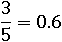
И умножим не эти две дроби, а равные им числа:
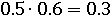
Получился такой же результат – значит все правильно
Еще пример:
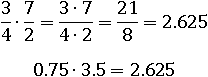
Нельзя забывать и об упрощающем арифметику основном свойстве дроби: в следующем примере в процессе умножения можно заменить 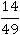 на равное ему, но более простое
на равное ему, но более простое 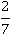 , что сильно упростит расчеты:
, что сильно упростит расчеты:
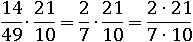
Применим основное свойство дроби еще раз, уменьшив числитель в 7 раз: для этого достаточно разделить 21 на 7 (разумеется, при этом с двойкой в числителе ничего делать не надо). Тогда и числитель, равный 42 (2∙21=42), уменьшится в 7 раз и станет равным 6 (2∙3=6). Точно таким же образом разделим на 7 и знаменатель:
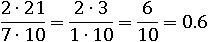
А что делать, если потребуется умножить дробь на число?
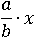
Тогда надо свести эту задачу к предыдущей, и сделать так, чтобы число x стало дробью, значение которой будет равно x. Например, если x разделить на 1, то получится дробь, равная x:
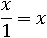
Или так:
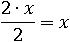
Действительно, два икса разделить на два – будет икс
Тогда заменим x на равную ему дробь:
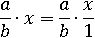
А как умножаются дроби уже известно:
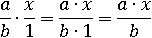
Например:
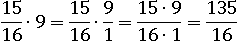
Деление дробей
Следует иметь ввиду, что в математике прежде всего ценится способность выводить правила и закономерности, а не способность эти правила запоминать! Поэтому попробуем именно вывести правило, по которому следует делить дроби. Тем более, что нижеописанная операция с многоэтажными дробями будет очень часто использоваться в математике далее.
Деление одной дроби на другую можно представить в виде четырехэтажной дроби, в которой числителем будет 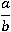 , а знаменателем
, а знаменателем 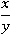 :
:
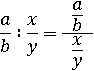
Воспользуемся основном свойстве дроби и умножим числитель 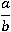 и знаменатель
и знаменатель 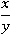 на число b:
на число b:
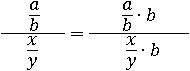
Теперь в числителе 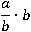 число a делится на b, а затем умножается на b. А что будет с числом, которое уменьшили в b раз и потом увеличили в b раз? Естественно число a от этого не изменится. Поэтому можно заменить
число a делится на b, а затем умножается на b. А что будет с числом, которое уменьшили в b раз и потом увеличили в b раз? Естественно число a от этого не изменится. Поэтому можно заменить 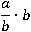 на a, потому что это одно и то же число:
на a, потому что это одно и то же число:
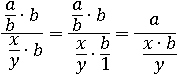
Дробь уже стала трехэтажной. Что бы сделать еще, чтоб она стала двухэтажной? Домножим опять, но уже на число y:
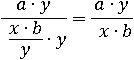
Получившееся выражение будет равно произведению двух дробей:
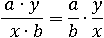
Так как к изначальному выражению мы применяли основное свойство дроби, которое не изменяет ее значение, то мы получили то же самое выражение только в другом виде:
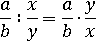
Вот таким образом из ничего благодаря логике мы вывели следующее правло:
Чтоб одну дробь разделить на другую, надо вторую дробь перевернуть, заменить деление умножением и умножить образававшиеся дроби:
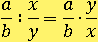
Пример:
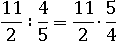
Ну а умножать дроби мы уже умеем:
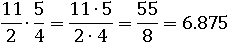
Проверить это можно, заменив дроби на равные им числа:
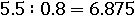
Еще пример:
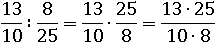
Упростим выражение, сократив с помощью основного свойства дроби:
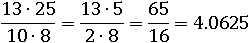
Деление дроби на число, которое дробью не является, происходит просто - x заменяется на равное ему число 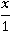 :
:
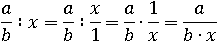
Приведем пример:
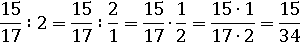
Сложение и вычитание дробей
Еще в математике очень полезным качеством является способность воспринимать один и тот же объект по-разному. Например, число можно воспринимать как количество кругов, изображенных на следующем рисунке.
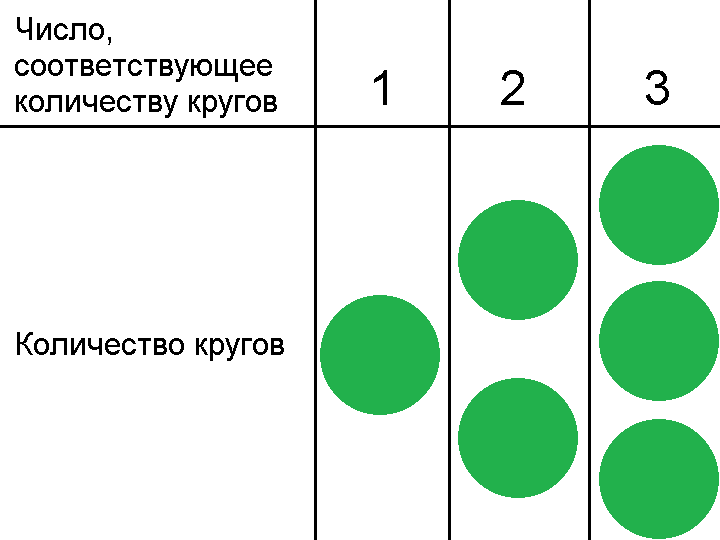
Тогда какое количество кругов будет соответствовать числу 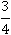 ? Это количество можно представить следующим образом: мысленно делим один круг на 4 равные части, и одну часть убираем. Таким образом, останутся только 3 части из 4. То есть это будет меньше одного круга.
? Это количество можно представить следующим образом: мысленно делим один круг на 4 равные части, и одну часть убираем. Таким образом, останутся только 3 части из 4. То есть это будет меньше одного круга.
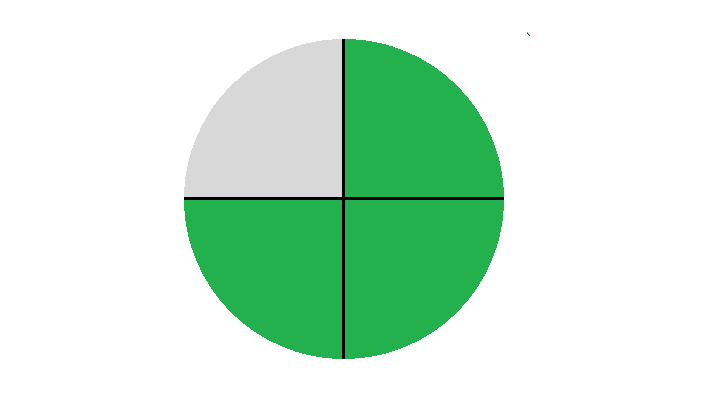
Числу 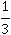 будет соответствовать окружность, поделенная на 3 равные части, из которых будет присутствовать только одна
будет соответствовать окружность, поделенная на 3 равные части, из которых будет присутствовать только одна
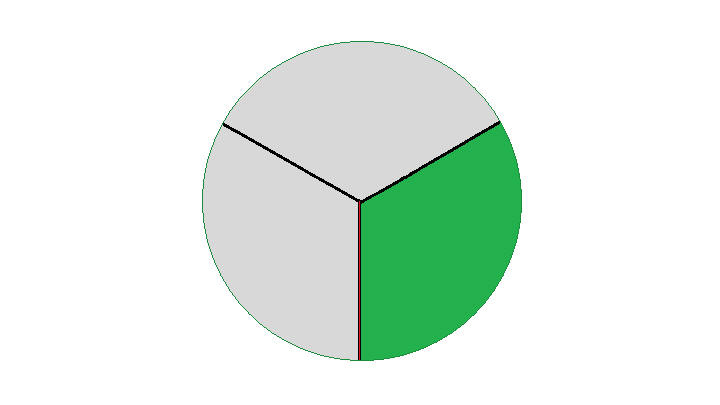
Сложим эти дроби:
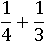
Количественно эту сумму можно изобразить в графическом виде:
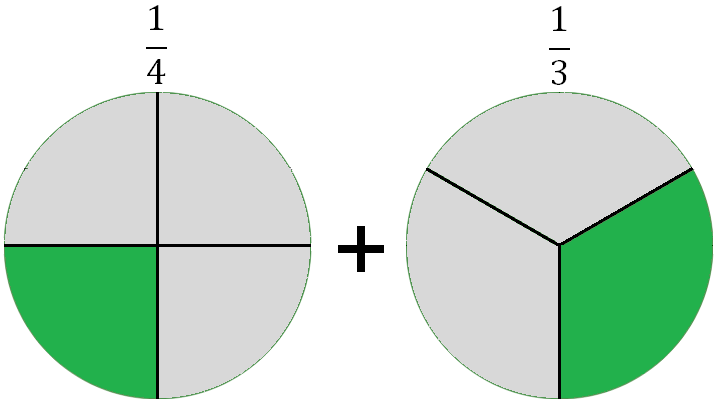
Теперь разделим каждую из присутствующих и отсутствующих долей первого круга на 3 равные части, а во втором круге каждую долю разделим на 4 равные части
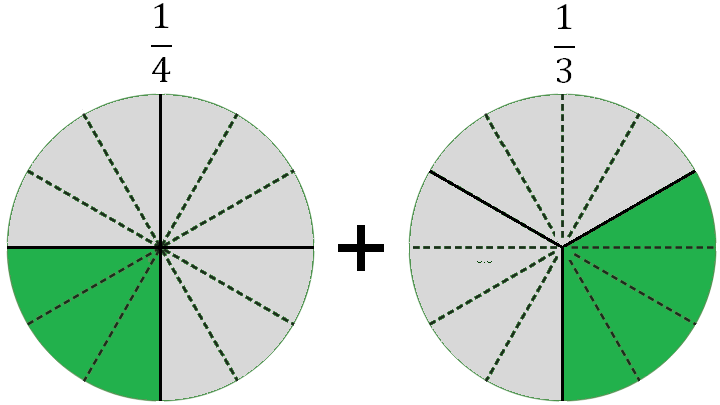
Такое преобразование равносильно применению основного свойства дроби: количество кругов и значения дробей не изменилось, а вид дробей стал другой – у них сейчас одинаковые знаменатели:
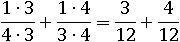
Каждый круг теперь поделен на 12 равных частей: 3 – в первом, и 4 – во втором. А значит, их можно сложить
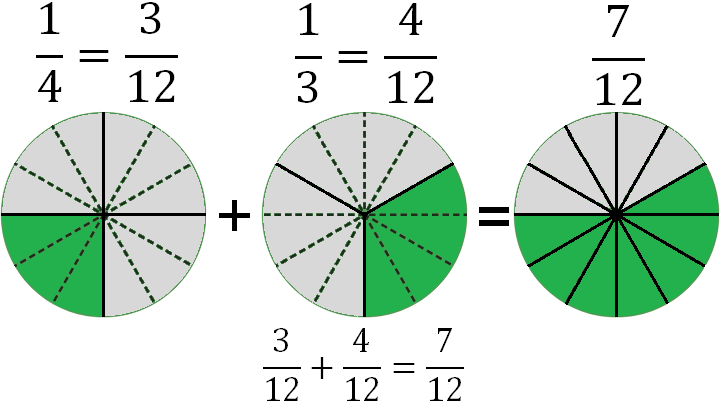
Таким образом, мы опять вывели новое правило:
Чтобы сложить дроби, нужно с помощью основного свойства дроби изменить вид дробей так, чтобы их знаменатели стали одинаковыми:
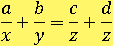
затем сложить числители, а новый общий знаменатель оставить тем же:
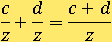
Применим на практике это правило:
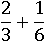
Легко можно заметить, что достаточно только домножить только первую дробь на 2, чтоб знаменатели стали одинаковыми:
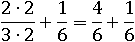
Осталось лишь сложить числители:
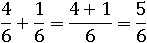
Так выглядет количественная аналогия
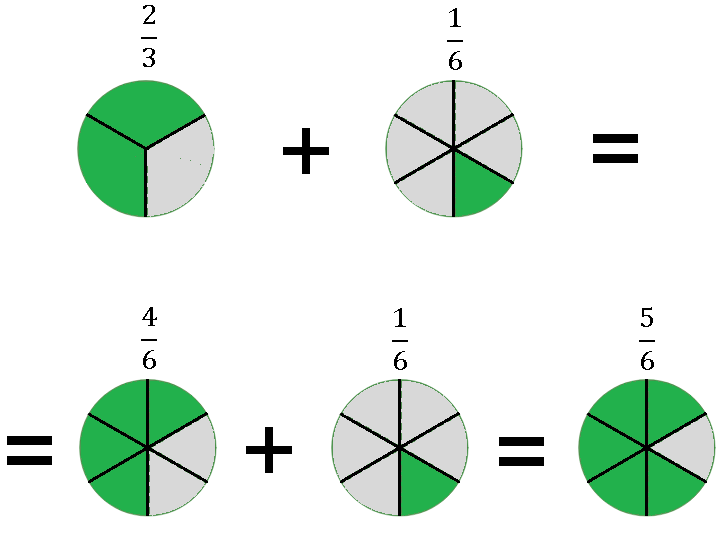
Чтобы отнять одну дробь от другой, сначала нужно тоже привести их к общему знаменателю:
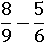
Первую дробь домножим на 2, вторую – на 3:
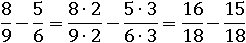
После чего отнимем от первого числителя второй:
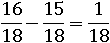
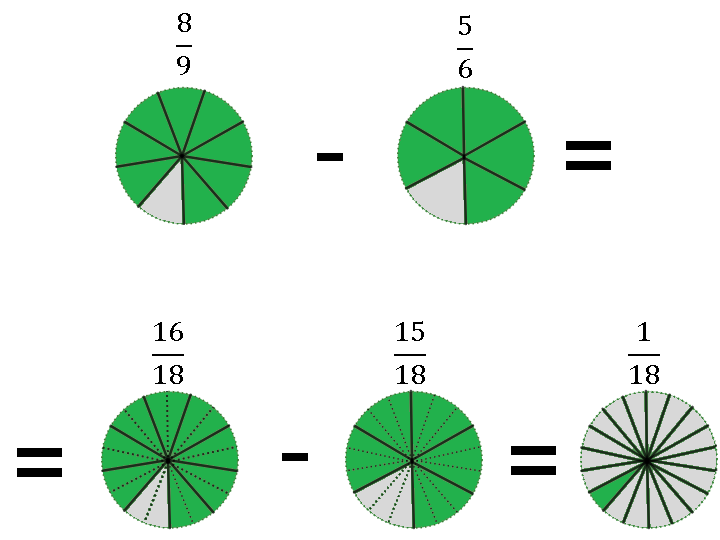
Все остальные действия с дробями будут основываться на вышеописанных правилах, поэтому не следует недооценивать их важность.