Квадратный корень
У каждой арифметической операции существует своя обратная, например, операцией обратной сложению является вычитание, действием противоположным умножению будет деление. В предыдущий раз мы изучали операцию возведения в квадрат, например, можно возвести в квадрат число 7, получив 49:
72=7∙7=49
Существует операция обратная возведению в квадрат – это извлечение арифметического квадратного корня из числа, благодаря которой мы можем из 49 назад получить число 7:
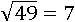
Чтобы извлечь арифметический квадратный корень из 49, нужно подобрать такое число, квадрат которого равен числу 49. Однако, существуют два таких числа – это 7 и −7:
72 = 7∙7 = 49
(−7)2 = (−7)∙(−7) = 49
Поэтому для определенности принято считать, что арифметическим квадратным корнем из действительного числа является именно неотрицательное число.
Так, например, квадратный корень из 16 будет равен 4, потому что 42=16, а число −4 не подходит, потому как оно отрицательное, несмотря на то, что его квадрат равен 16:
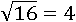
Можно ли извлечь квадратный корень из отрицательного числа, например из −16? Для этого нужно найти число, которое в квадрате равно −16, то есть число, которое при умножении на само себя будет равно −16. Но если умножать какое-нибудь положительное число на само себя, то неизбежно получится положительное число, а если отрицательное умножать на отрицательное, то получится опять положительное.
Получается, что среди уже известных нам действительных чисел нет таких, квадрат которых равен отрицательному числу. А вот среди неизвестных комплексных чисел такие числа существуют, только, чтоб приступить к их изучению нужно для начала хотя бы узнать что такое синус и косинус на единичной окружности. Так что пока мы не выйдем за пределы школьной программы, мы будем считать извлечение квадратного корня из отрицательного числа невыполнимой операцией.
Поэтому следующее определение распространяется только на неотрицательные числа.
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a:
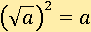
Число a, находящееся под знаком корня, называется подкоренным числом. Для краткости слово «арифметический» часто опускают, а иногда говорят просто «корень из a».
Квадратный корень можно извлечь и из нецелого положительного числа, главное, чтоб оно было неотрицательным:
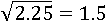
Очевидно, что квадратный корень из нуля и единицы тоже будет равен нулю и единице:
Далеко не из всех неотрицательных чисел возможно точно извлечь корень, а можно получить только его приближенное значение тогда, обычно, говорят, что корень не извлекается.
Например, не получится точно извлечь корень из семи:
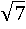
Какое число при умножении на себя будет равно семи? 2 – мало, 3 – много, значит где-то больше двух, но меньше трех:
Корень из семи приблизительно равен такому числу:
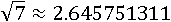
На самом деле число 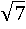– иррациональное, значит цифры после запятой будут идти до бесконечности, а бесконечное количество цифр написать невозможно. Так что корень из семи можно вычислить всегда только приблизительно. В таких случаях не пытаются извлечь корень, а так его и оставляют, имея ввиду такое число, квадрат которого равен семи.
Такие числа как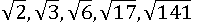 
и. т. д тоже иррациональные, поэтому можно получить только приближенные значения корней из этих чисел:
Извлечение квадратного корня в столбик
В процессе изучения математики редко придется сталкиваться с большими числами, а среди маленьких чисел не так много тех из которых корень извлекается, поэтому корень из таких чисел либо просто уже помнят, либо его легко можно подобрать. Если же корень из числа не извлекается, (как правило, это сразу заметно), тогда его и не требуется извлекать.
Но все же иногда приходится извлекать корень из большого числа или получать его приближенное значение без калькулятора, поэтому рассмотрим на примере способ извлечения квадратного корня в столбик.
Допустим нам нужно извлечь квадратный корень из числа 241081. Напишем это число вместе с десятичной запятой, которая в этом числе идет сразу после цифры 1 и вертикальную черту справа, после которой будем потом записывать цифры результата. Затем, начиная с запятой, разобьем все число на группы разделителем – по две цифры в каждой. Количество таких групп равно количеству цифр в будущем извлеченном корне.
Подбираем наибольшее однозначное число, квадрат которого меньше либо равен числу 24 в первой группе, таких чисел всего десять:
02=0∙0=0 52=5∙5=25
12=1∙1=1 62=6∙6=36
22=2∙2=4 72=7∙7=49
32=3∙3=9 82=8∙8=64
42=4∙4=16 92=9∙9=81
Выходит, что наибольшим числом, не превосходящим 24, является 16, а 25 – уже больше чем 24 и не подходит. Значит, под 24 в первой группе записываем 16, и под 16 проводим черту.
Число 16 мы получили, когда возводили в квадрат 4, значит, справа от вертикальной черты записываем 4 – это первая цифра результата.
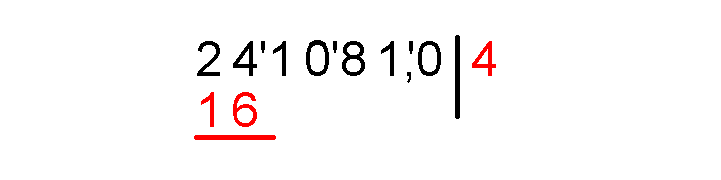
Отнимаем столбиком от 24 число 16, проводим горизонтальную черту и под ней записываем результат равный восьми.
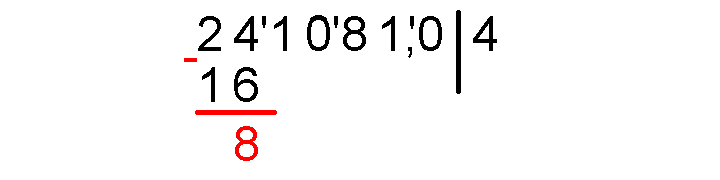
Приписываем к этой восьмерке вторую группу, чтобы под нижней чертой получилось число 810, которое мы напишем синим цветом, и слева от него проведем вертикальную черту.
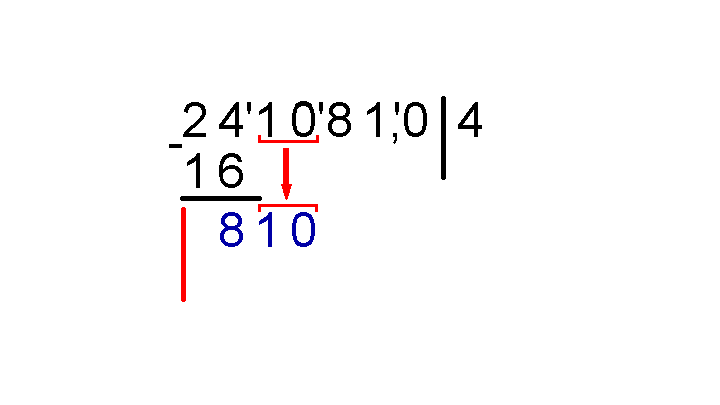
Возьмем имеющуюся часть результата (число 4) и умножим ее на 2, результат этого умножения равный восьми запишем справа от вертикальной черты так, чтобы после этой восьмерки осталось место для еще одной цифры.
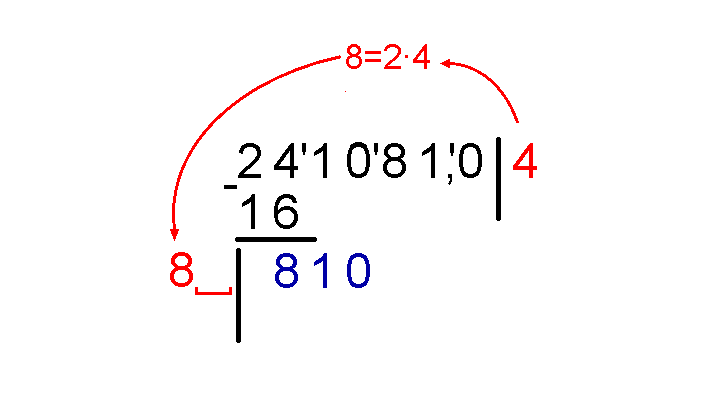
Теперь к этой восьмерке нужно приписать одну цифру, так чтобы получилось двухзначное число, после чего умножить это двухзначное число на цифру, которую приписали. Например, если приписать к этой восьмерке цифру 2 и умножить на 2, то получится 164:
82∙2=164
А если приписать 3, то получится 249:
83∙3=249
И так далее:
84∙4=336 87∙7=609
85∙5=425 88∙8=704
86∙6=516 89∙9=801
Из получившихся трехзначных чисел нужно выбрать наибольшее, которое не будет превосходить синего числа 810. Подходит 801, потому что, оно самое большее из тех чисел, которые меньше чем синее 810.
Число 801 получилось в результате умножения 89 на 9, значит, 9 – это вторая цифра результата, написать ее надо в трех местах – после четверки в результат, в оставленное после восьмерки место и еще раз под этой же девяткой.
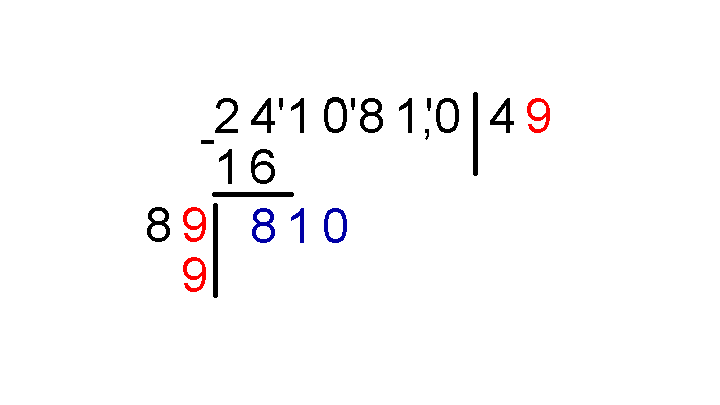
Производим умножение 89∙9 в столбик. Только результат умножения 89∙9 следует записывать под синим 810.
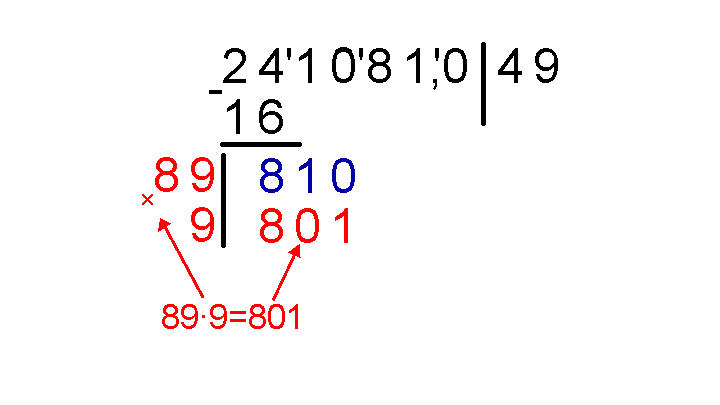
Подведем черту под 801 и столбиком отнимем 801 от 810. К получившемуся результату вычитания (числу 9) припишем следующую группу, образовалось число 981, которое мы также выделим синим цветом.
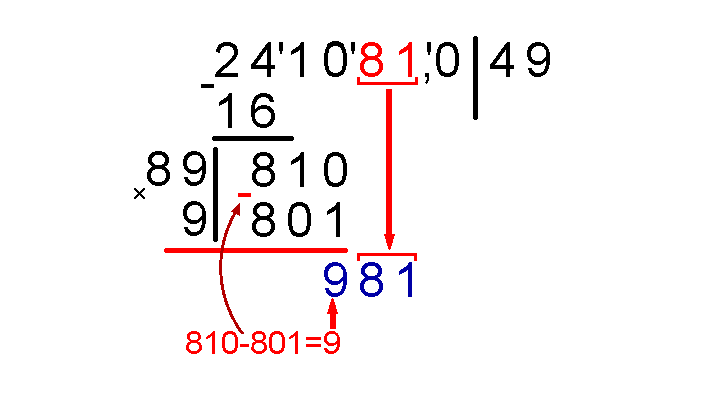
Далее все повторяется. Ставим вертикальную черту слева от синего 981. Опять умножаем имеющуюся сейчас часть результата (это уже 49) на 2, получаем 98, пишем 98 слева от вертикальной черты, оставляя место для еще одной цифры.
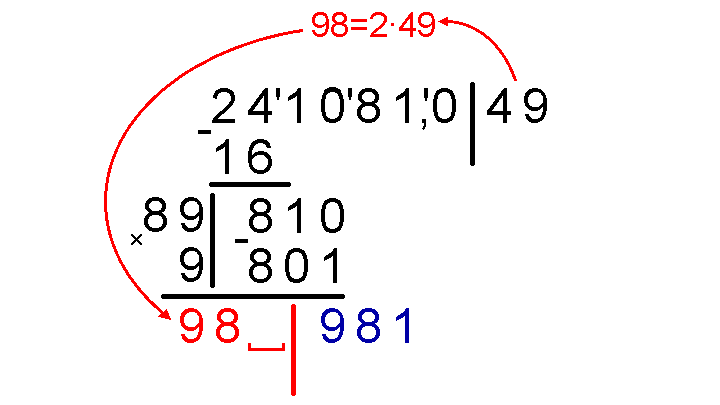
И подбираем, наибольшую цифру, которую следует приписать к 98. чтобы после умножения 98 с этой приписанной цифрой на эту же цифру получилось число меньшее или равное синему 981:
980∙0=0
981∙1=981
982∙2=1964
…
Тут сразу можно увидеть, что приписать нужно единицу, потому что 981, умноженное на приписанную единицу, как раз будет равно синему числу 981. Следовательно, 1 – это очередная цифра результата, напишем 1 в трех местах: после 49, после 98 в оставленное место и еще раз под этой же единицей. .
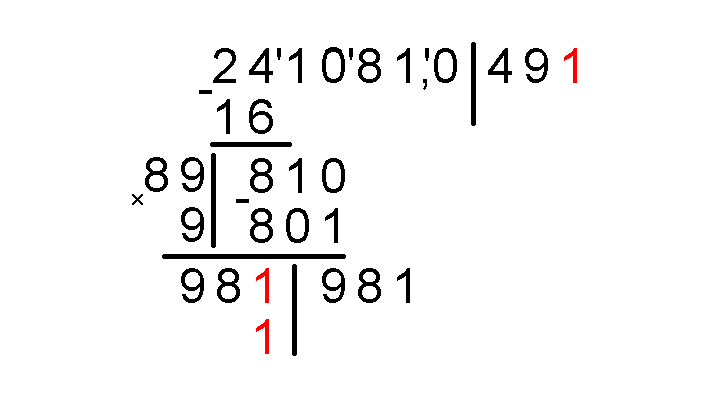
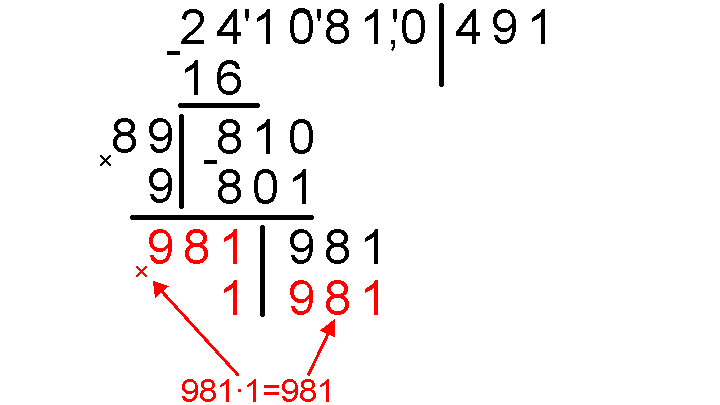
Умножаем в столбик 981 на 1, результат умножения записываем под 981.
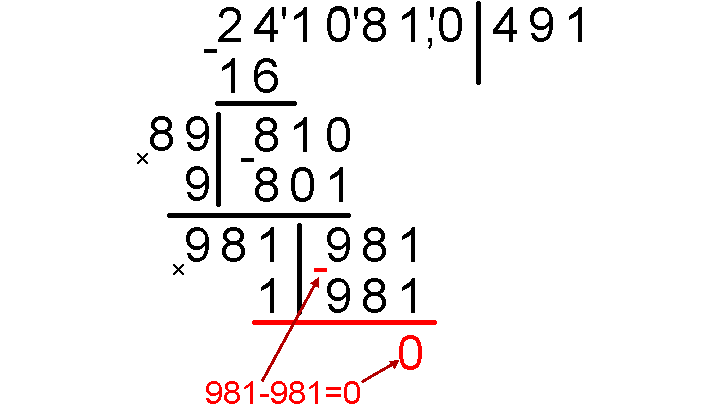
Проводим горизонтальную черту под 981 и отнимаем 981 от 981, будет ноль – это значит, что весь процесс завершен, и корень из числа извлекается. Если до нуля дойти так и не удалось, значит, корень не извлекается и получить можно лишь приближенное значение, либо где-то была допущена ошибка.
Проверим результат возведением в квадрат 491:
4912=491∙491=241081
Полученное число совпало с первоначальным – все правильно.
Теперь извлечем корень в столбик из 41, корень из этого числа не извлекается, поэтому вычислим его приблизительно – только первые три цифры после запятой. Для этого после запятой напишем еще шесть нулей, по два нуля на каждый знак после запятой в будущем приближенном корне.
Начиная с запятой, разделим все число на группы по две цифры и поставим вертикальную черту, после которой будем записывать результат.
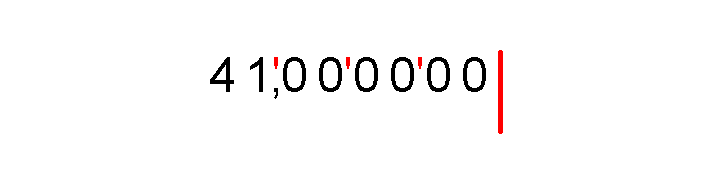
Подбираем наибольшую цифру, квадрат которой меньше или равен 41:
02=0∙0=0 52=5∙5=25
12=1∙1=1 62=6∙6=36
22=2∙2=4 72=7∙7=49
32=3∙3=9 82=8∙8=64
42=4∙4=16 92=9∙9=81
Очевидно, что подходит число 6, квадрат которого равен 36. Значит, после вертикальной черты ставим 6, а под 41 пишем 36.
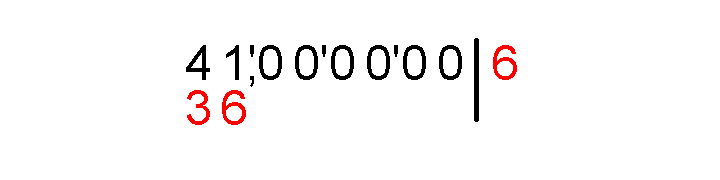
Отнимаем столбиком 41−36, записываем полученную разницу равную пяти, и рядом пишем следующую группу, состоящую из двух нулей.
Поскольку мы уже начали приписывать группы находящиеся за пределами запятой в числе 41, то следует поставить запятую и после шести.
.
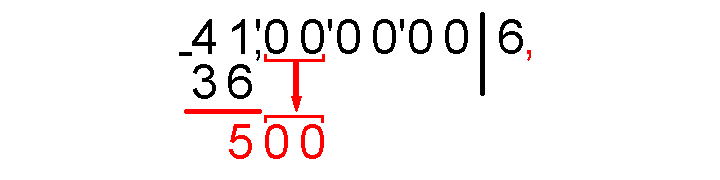
Умножаем на два часть результата, который уже есть, и получившееся 12 записываем, оставляя место для одной цифры.
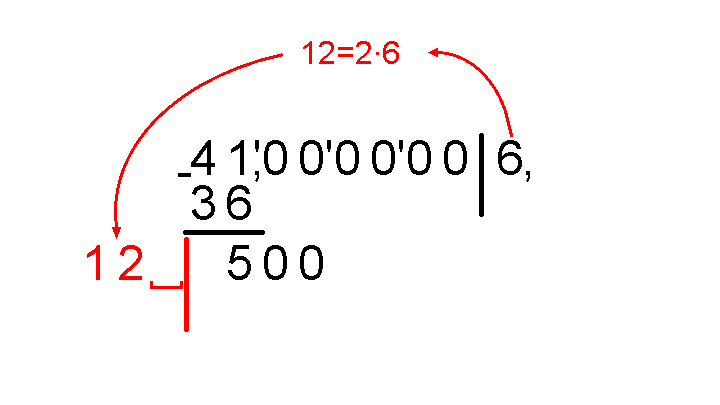
Подбираем цифру, которую надо приписать к 12. Подходит 4, потому что 124∙4=496 – это наибольший результат не превосходящий 500. Пишем цифру 4 и в результат после запятой, и после 12, и ниже 12-ти.
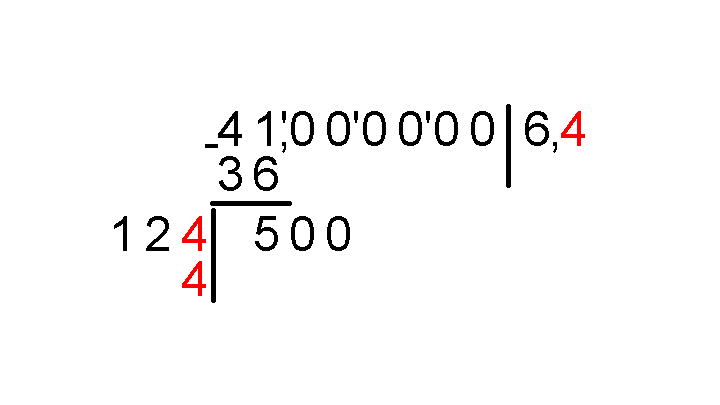
Умножаем столбиком 124 на 4, результат записываем под 500.
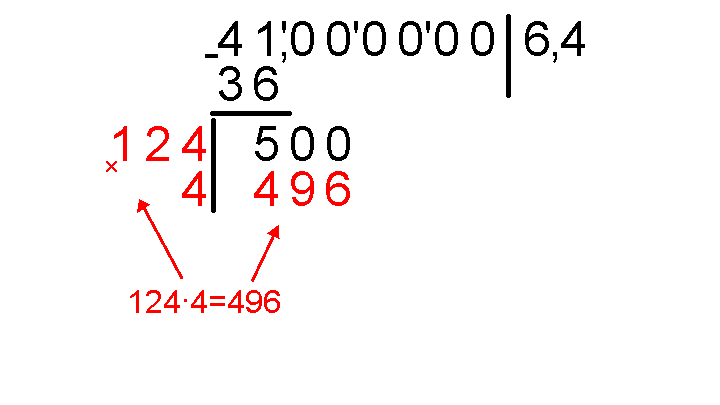
Отнимаем 500−496, результат записываем под очередной горизонтальной чертой и сносим следующую пару нулей.
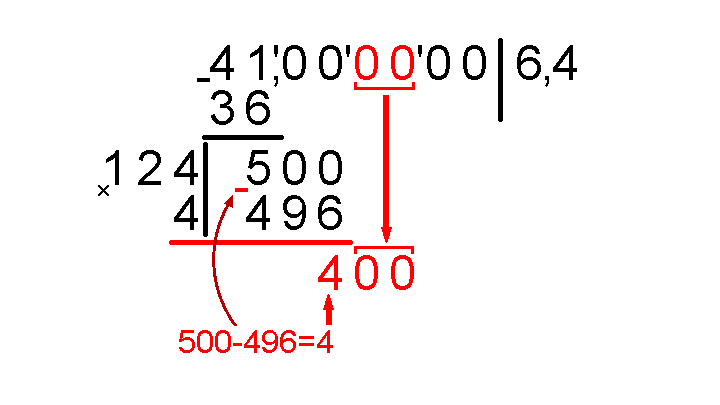
Снова умножаем на два весь существующий результат без учета запятой: 64∙2=128. Записываем 128, оставив место для еще одной цифры.
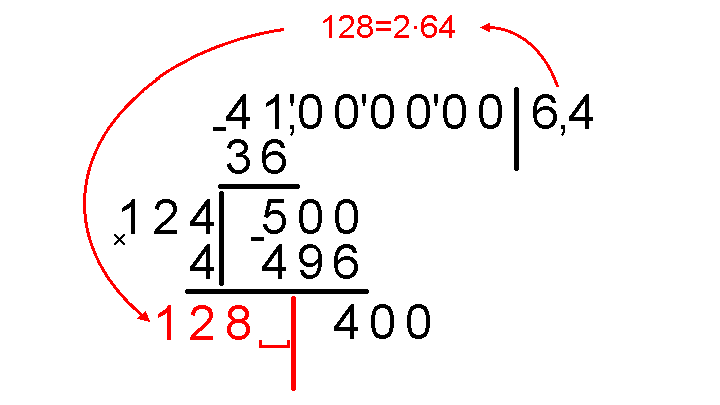
Дальше нужно подбирать цифру, которую нужно поставить после 128. Но даже если подставить единицу и на нее умножить, получится слишком много – гораздо больше чем 400:
1281∙1=1281
Но существует цифра, значение которой еще меньше одного – ноль:
1280∙0=0
Следовательно, следующая цифра результата – ноль. Ставим этот ноль во все нужные три места.
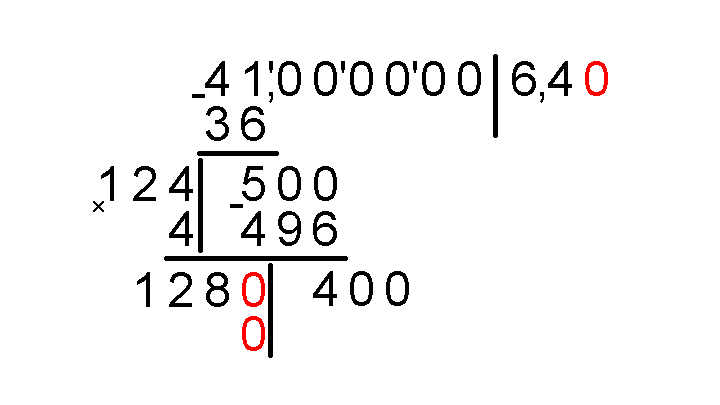
Умножаем 1280 на 0, результат записываем под 400.
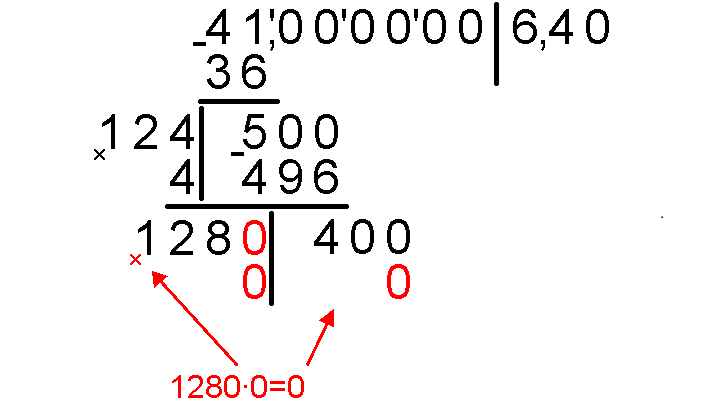
Столбиком вычитаем 0 из 400, приписываем к разности следующую группу, состоящую из нулей.
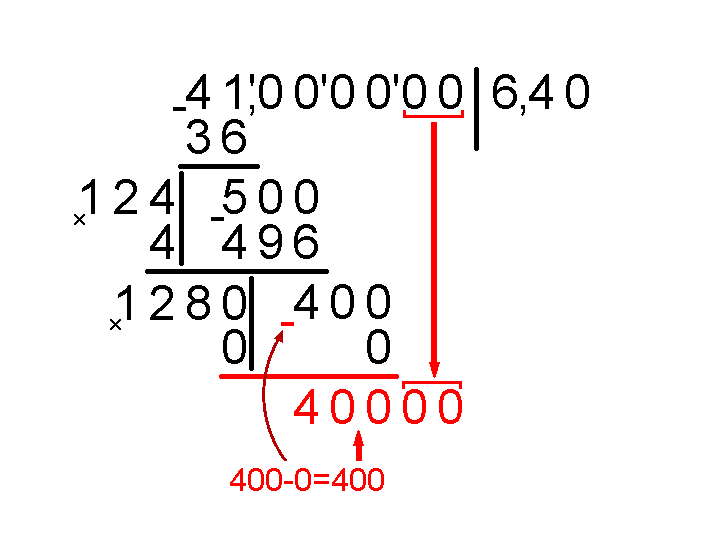
Умножаем на два имеющуюся часть результата: 640∙2=1280, записываем слева 1280, оставив место под следующую цифру.
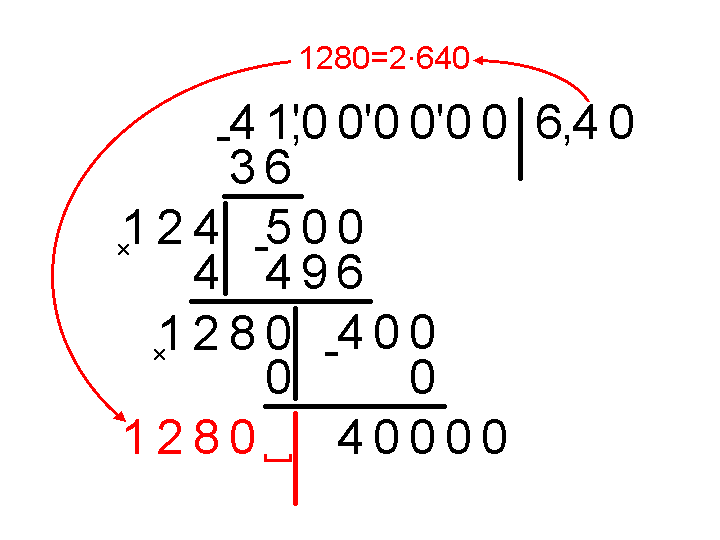
Если приписать к 1280 еще одну цифру получится больше чем 12 тысяч. Значит, умножить его надо на 3, чтобы получилось максимальное число не превосходящее 40 тысяч. Следовательно, следующая цифра результата – три.
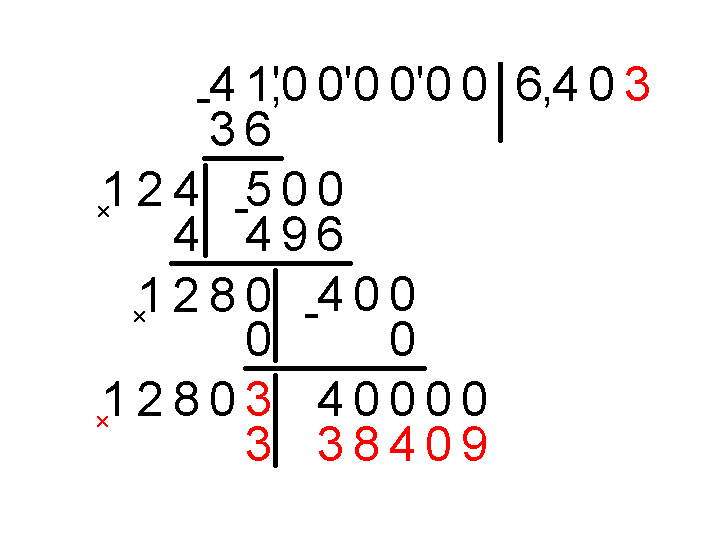
Так как корень из 41 не извлекается, то процесс извлечения корня из этого числа можно продолжать до бесконечности, с каждым разом увеличивая точность. Но мы собирались найти только первые три цифры после запятой.
Осталось только убедиться, что квадрат числа 6.403 достаточно близок к 41:
6.4032=40.998409
Значит, корень из 41 приблизительно равен:
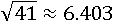
Этот метод имеет один недостаток – каждый следующий шаг будет сложнее предыдущего. Чтобы получить более точный результат придется каждый раз умножать и отнимать все более крупные числа. Например, так:
