Степень с отрицательным целым показателем

• Показатель равный нулю
• Дробь в отрицательной степени
• Примеры

Показатель степени – не только количество перемножений

Можно ли возвести число 2 в отрицательную степень, например в минус вторую степень? Если возведение числа 2 во вторую степень – это умножение этого числа на себя 2 раза, то как можно умножить число 2 на себя минус два раза? Но совсем не обязательно воспринимать показатель исключительно как количество перемножений, можно посмотреть на него с несколько другой точки зрения.

Возьмем число 2, и умножим его на два, а то, что получится запишем справа от 2:

2;   4

Затем возьмем последнее число в этой последовательности и тоже умножим его на два: 4∙2=8, и припишем 8 справа от числа 4:

2;   4;   8

И опять: берем последнее число 8, умножаем его на два и приписываем 16 в конец последовательности:

2;   4;   8;   16

Так можно сколько угодно удлинять вправо эту последовательность:

2;   4;   8;   16;   32

2;   4;   8;   16;   32;   64 ...

В итоге мы имеем следующую последовательность возрастающих чисел, где каждое следующее больше предыдущего в два раза:

2;   4;   8;   16;   32;   64

А как следует действовать, чтобы добавить еще одно число, но уже к другому (к левому) концу последовательности. Какое число следует поставить перед двойкой, чтобы каждое следующее оставалось в два раза больше предыдущего?

???;   2;   4;   8;   16;   32;   64

Очевидно, для этого следует производить обратную операцию – деление на два первого числа в последовательности. Разделим на 2 первое число в последовательности: 2∶2=1, и запишем 1 перед 2:

1;   2;   4;   8;   16;   32;   64

Логика происходящего в последовательности процесса сохранилась: каждое следующее число по-прежнему больше предыдущего в два раза, включая число 1.

Добавим еще одно число слева, которое можно получить, разделив 1 на 2:

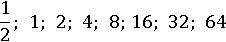
Чтобы продолжить, нужно уже 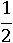разделить на 2:

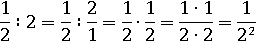
Запишем 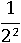перед 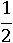, в результате получим такую последовательность:

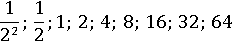
В левую сторону последовательность также можно расширять до бесконечности:

На будущее будет полезным заметить: по мере расширения последовательности влево числа будут становиться все меньше и меньше, все ближе приближаясь к нулю, но при этом они будут оставаться положительными.

Вы, наверное, уже заметили, что некоторые числа в этой последовательности являются степенями двойки:

21=2

22=2∙2=4

23=2∙2∙2=8

...

26=2∙2∙2∙2∙2∙2=64

Занесем эти данные в следующую таблицу. Часть нижней строки заполним числами из нашей последовательности, которые являются степенями двойки.

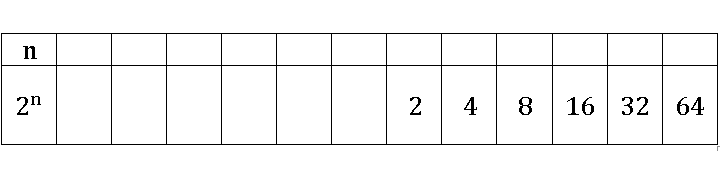
И над каждым числом запишем соответствующий ему показатель этой степени. Например, 23=8, значит, над 8 напишем 3, 24=16, значит, над 16 напишем 4 и т. д.

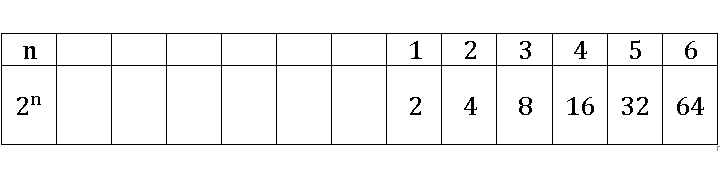
Занесем и остальные числа из последовательности в таблицу в том же порядке.

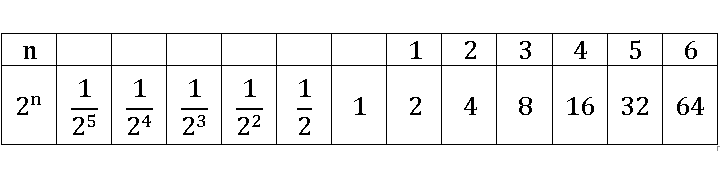
Верхняя строка оказалась заполненной не полностью, поэтому заполним пустые ячейки так, чтобы числа в ней продолжали возрастать на единицу.

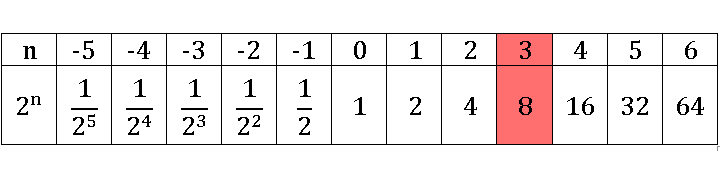
Эта таблица ставит в соответствие показателю n число 2n. Например, выделенный красным столбец говорит, что два в степени 3 равно 8. Также с помощью таблицы уже можно определить что получится, если 2 возвести в отрицательную целую степень:

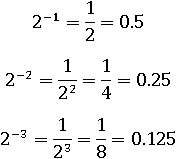
И уже становится заметной новая закономерность: степень с отрицательным показателем равна единице, деленой на ту же степень, только с уже положительным показателем. Теперь мы можем обобщить эту закономерность на любой отрицательный целый показатель и любое основание не равное нулю:

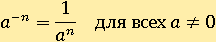
В отрицательную целую степень можно возводить любое число a кроме нуля, чтобы в вышеописанной формуле не получилось деления на ноль.

Вот примеры использования этой формулы:

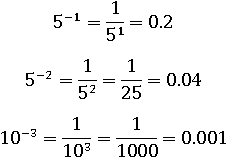
Все свойства степени будут теперь верны не только при натуральном показателе, но и при целом показателе.

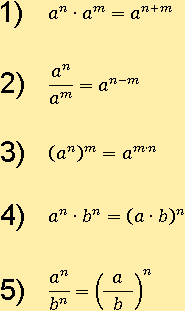
Во втором свойстве уже нет ограничения n>m, потому что теперь нет никакой необходимости в положительном показателе, как это было в свойсвах степени с натуральным показателем.

Мы можем следующее выражение упростить так:

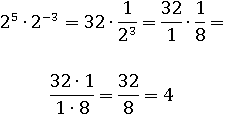
А можем применить первое свойство степени и сложить показатели. Получится тоже 4:

25∙2−3=25−3=22=2∙2=4

Показатель равный нулю

Отдельно стоит упомянуть о показателе равном нулю. Таблица говорит, что 20=1. И действительно, на самом деле не только 2, но и любое число (кроме нуля) в степени ноль равно единице. Вспомним, откуда в таблице взялась эта единица. Она получилась, когда мы делили 2 на 2, т. е. делили основание 2 на само себя, а любое число (кроме нуля) деленое на само себя будет равно единице. Поэтому нельзя ноль возводить в степень ноль – на ноль нельзя делить никакое число, и ноль на ноль тоже делить нельзя.

Если составить таблицу по тому же принципу, но с другим основанием, то мы также получим единицу при n=0. Например, в нижеследующей таблице основанием является число 3.

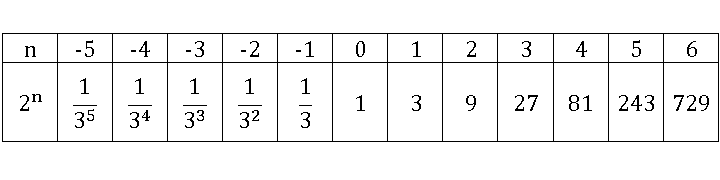
Дробь в отрицательной степени

Выведем одно полезное свойство отрицательного показателя. Возведем в степень –n дробь:

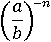
Избавимся от минуса в показателе:

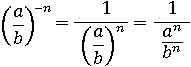
С помощью основного свойства дроби и пятого свойства степени сделаем из трехэтажной дроби двухэтажную, умножив на bn числитель и знаменатель:

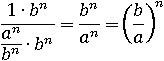
Получилось следующее свойство:

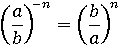
Например:

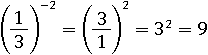
Значит, чтоб поменять знак показателя достаточно просто перевернуть дробь.

Примеры

Вот несколько примеров упрощения выражений с отрицательными целыми показателями.

Пример № 1

4−2∙5−3

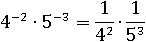
Умножим дроби

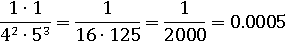
Пример № 2

0.5−3∙0.5−4

Первый способ.

Избавимся от минусов в показателях, применив формулу:

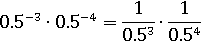
Возведем 0.5 в третью и четвертую степени, затем умножим дроби:

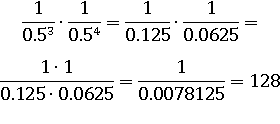
Второй способ.

Но все свойства степени прекрасно выполняются и для отрицательных показателей. Поэтому можно было упростить, используя первое свойство степени и просто сложить показатели:

0.5−3∙0.5−4=0.5−3+(−4)=0.5−7

Число 0.5 равно одной второй, значит можно заменить 0.5 на одну вторую:

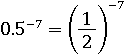
Нам уже известно, что можно перевернуть дробь, поменяв знак показателя:

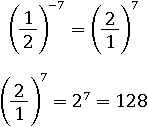
Пример № 3

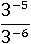
Применим второе свойство степени и отнимем показатели:

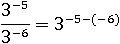
Отнять −6 от −5 – это тоже самое, что и прибавить 6 к −5:

3−5−(−6)=3−5+6=31=3

Пример № 4

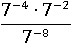
Воспользуемся первым свойством степени, чтобы упростить числитель:

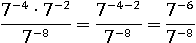
И применим второе свойство степени:

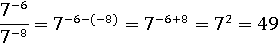
Пример № 5

(2−2)−3

Первый способ.

Можно избавиться от минуса сначала в одном показателе:

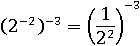
Потом в другом:

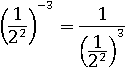
Затем возвести дробь в знаменателе в третью степень:

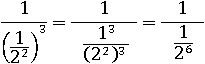
И упростить выражение, применив основное свойство дроби:

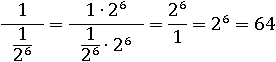
Второй способ.

Но можно сэкономить время благодаря третьему свойству степени:

(2−2 )−3=2(−2∙(−3))=26=64

Не стоит думать, что первый способ не представляет ценности, всегда полезно видеть разные методы решения задачи.

Пример № 6

(x3−x2 )∙x−2

Раскроем скобки:

(x3−x2 )∙x−2 = x3∙x−2−x2∙x−2

Сложим степени с помощью первого свойства степени:

x3∙x−2−x2∙x−2 = x3−2−x2−2

x3−2−x2−2 = x1−x0 = x−1

Изначальное выражение равносильно конечному для всех не равных нулю x:

(x3−x2 )∙x−2 = x−1

Но работать с конечным выражением намного легче, а в силу их равносильности результат будет одинаковым. Сравним удобство вычисления значения этого выражения при x=2 у начального выражения и его упрощенной конечной версией.

Вычисление значения начального выражения:

(x3−x2 )∙x−2=(23−22 )∙2−2=

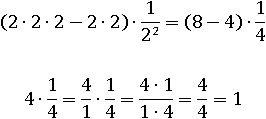
А вот значение упрощенного варианта получить совсем легко:

x−1=2−1=1

Попробуйте также подставить вместо x любое другое число кроме нуля в оба выражения, и вы получите совершенно одинаковый результат.

© Кирилл Морковкин & Машка Кулибякина