Тангенс
Такие тригонометрические функции как тангенс и котангенс используется реже чем синус и косинус, но понимать, что они из себя представляют все же необходимо. Точное школьное определение гласит:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
Легче это будет понять на примере. Попробуем приблизительно вычислить тангенс 30-ти градусов. Для этого нам нужно начерить прямоугольный треугольник (т.е. такой треугольник, в котором один угол будет 90°), пусть прямым углом будет угол C. В нашем треугольнике АВС угол А=30°, сторона ВС=5,8 см (катет противолежащий углу А), а сторона АС=10 см (катет прилежащий углу А).
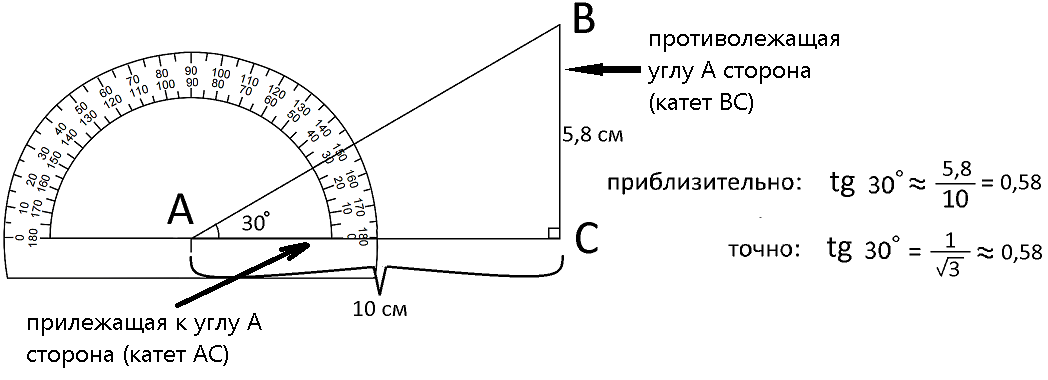
Тангенс угла А получится, если длину стороны, противолежащей углу А, разделить на длину стороны, прилежащей углу А. То есть, если 5,8 разделить на 10. После деления 5,8 на 10, получим 0.58, приблизительно это число и есть тангенс угла 30°. Таким образом tg 30° ≈ 0,58. Разумеется, так тангенс никто не считает, но подобныое объяснение очень наглядно. Точное значение tg 30° таким способом определить не удастся, потому что невозможно абсолютно точно измерить катеты или начертить идеально правильный прямоугольный треугольник. На самом деле точные значения тангенса углов 30°, 45°, 60° придется просто запомнить, а тангенсы других углов от 0° до 90° для решения школьных задачь просто никогда не понадобятся. Таблица с точными значениями тангенса и котангенса этих углов будет дана ниже.
Найдем tg 45° сначала через прямоугольный треугольник, а затем проверим полученный результат на калькуляторе. Начертим прямоугольный треугольник с углом 45°,измерим в нем катеты и разделим длину катета BC, противолежащего углу 45° на длину катета AC, прилежащего углу 45°, т.е. разделим 10 на 10 - получим 1, значит tg 45°=1.
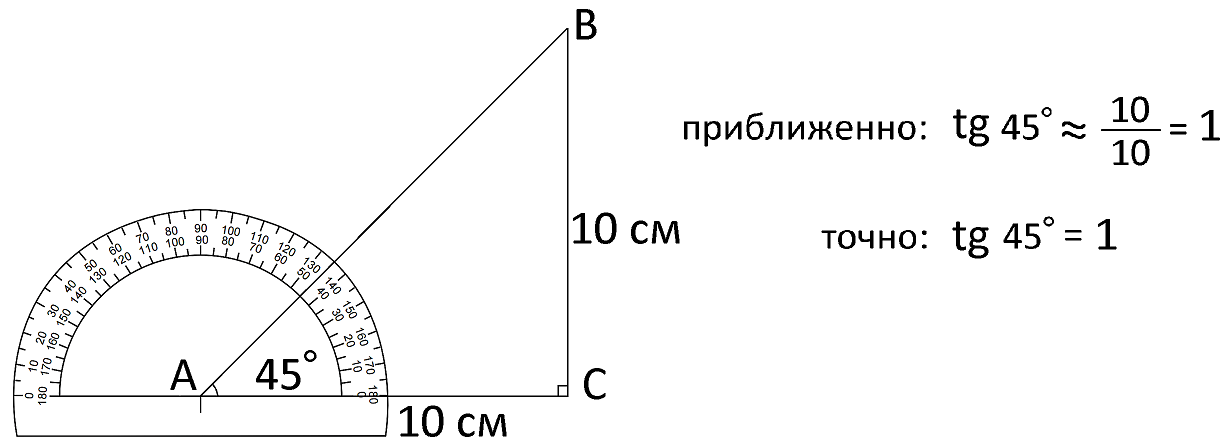
Более точное (но все же обычно только приближенное) значение тангенса можно найти с помощью калькулятора. Посмотрим согласится ли с нами калькулятор.
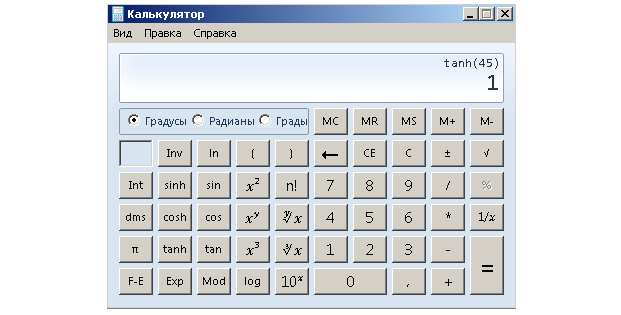
В этот раз нам удалось абсолютно точно определить tg 45° и калькулятор также выдал абсолютно правильное значение tg 45°. Посмотрим удастся ли это нам и калькулятору в следующий раз.
Таким же способом определим tg 60° сначала с помощью прямоугольного треугольника.
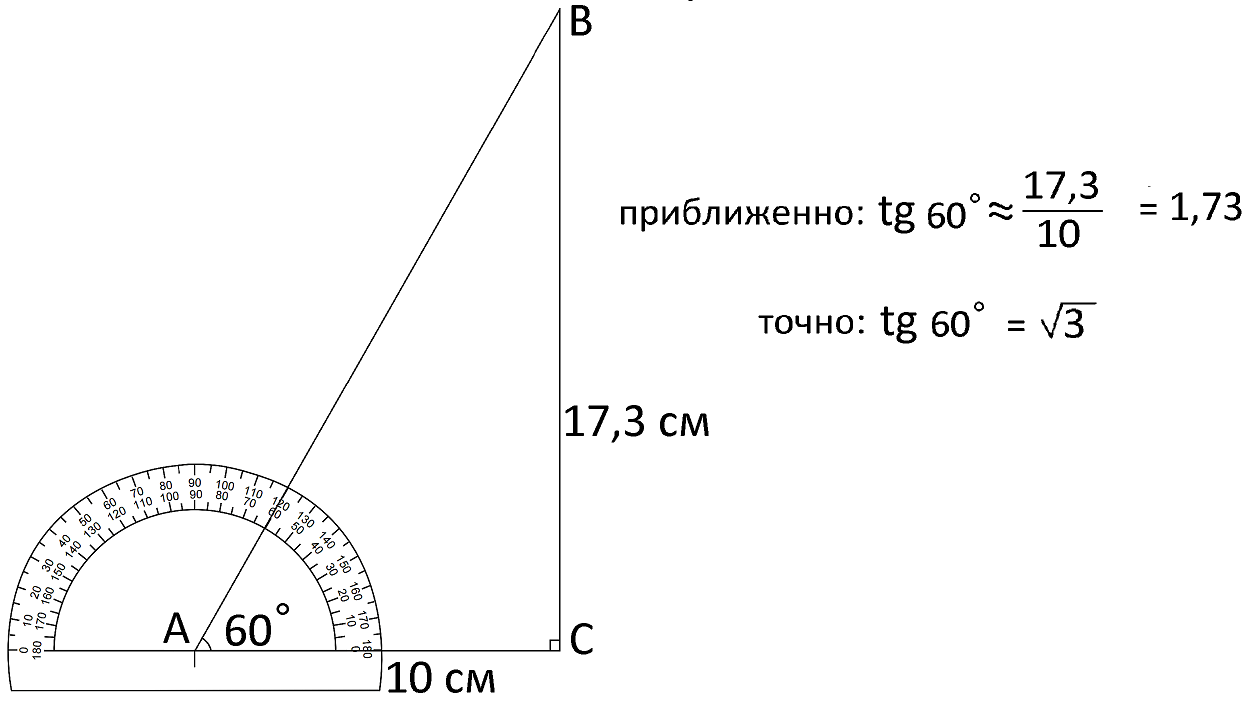
Результаты наших вычислений и калькулятора близки, но не точны, на самом деле абсолютно точное значение tg 60° равно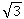 
(квадратному корню из трех), это число невозможно написать абсолютно точно, потому что цифры после запятой в этом числе будут идти до бесконечности.
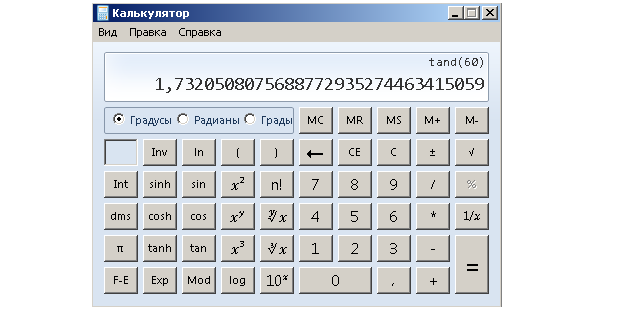
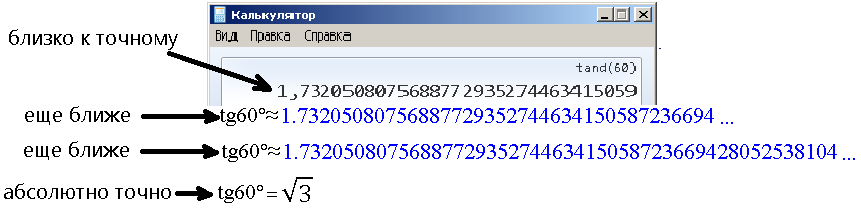
Можно только приближаться точному результату, добавляя цифры, но это все равно будет приближенное (хоть и очень похожее на истинное) значение tg 60°
Котангенс
Котангенс не меньше похож на тангенс, чем синус на косинус, между ними тоже наблюдается некая симетрия:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
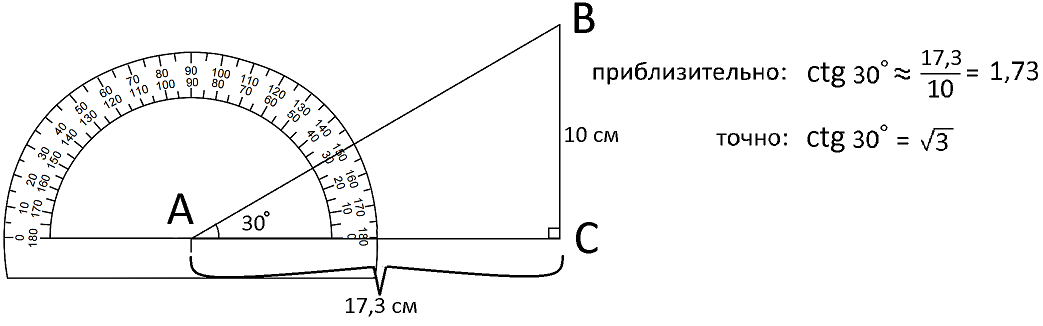
Котангенс отличается от тангенса тем, что делить надо наоборот - прилежащую углу А сторону AC на противолежащую BC. Получается, что, например, котангенс 30° равен 17,3 деленому на 10, и таким образом котангенс 30° будет приблизительно равен 1,73.
Пример приближенного определения котангенса 45° изображен на следующем рисунке.
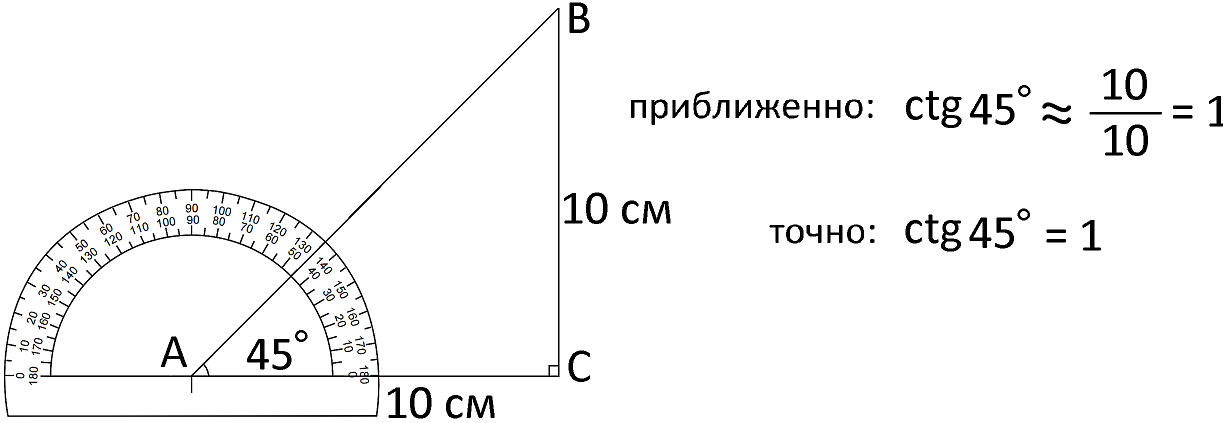
Должно быть совершенно очевидно, что tg 45° и сtg 45° оба равны единице, т.к. если противолежащий катет при делении на прилежащий равен единице, то и прилежащий катет при делении на противолежащий будет равен единице.
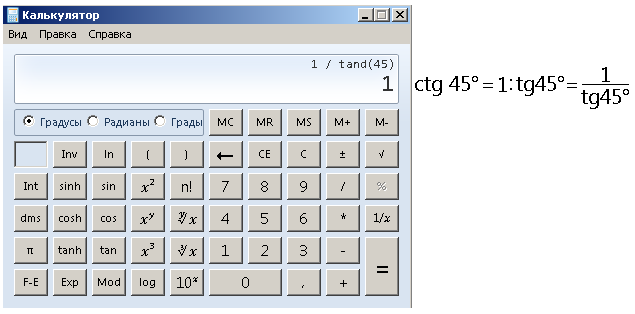
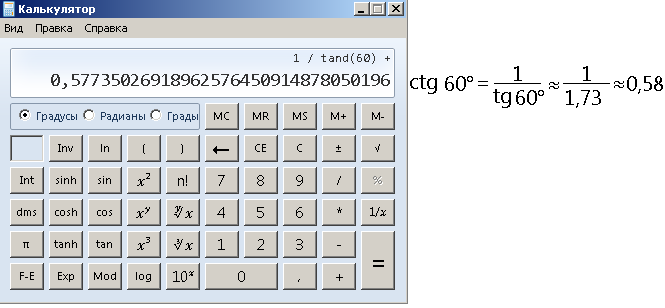
Котангенс на столько похож на тангенс, что его даже никогда нет на калькуляторе. Чтобы вычислить ctg 45° на калькуляторе надо единицу разделить на tg 45°.
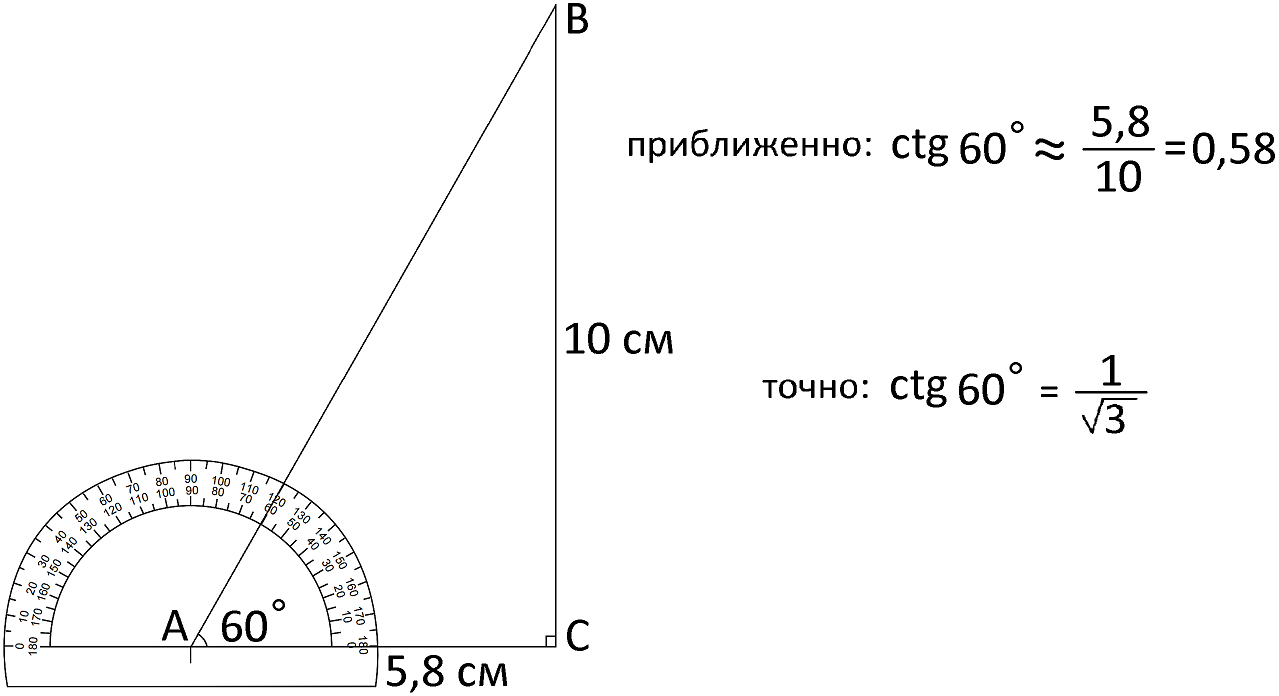
Аналогичным способом приближенно вычисляем ctg 60°.
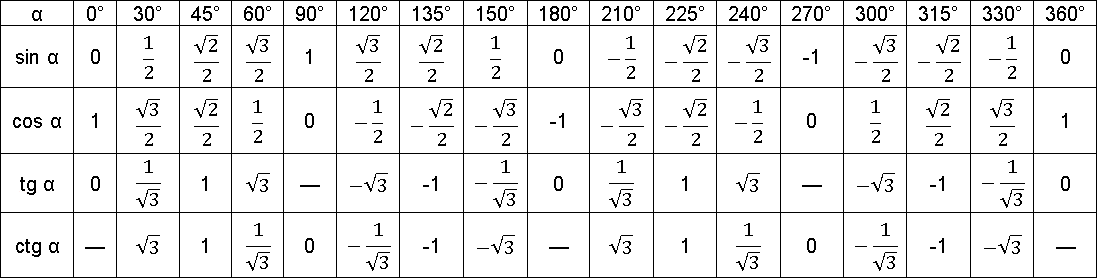
Все нужные точные значения тангенса и котангенса, которые надо знать, заключим в таблицу.
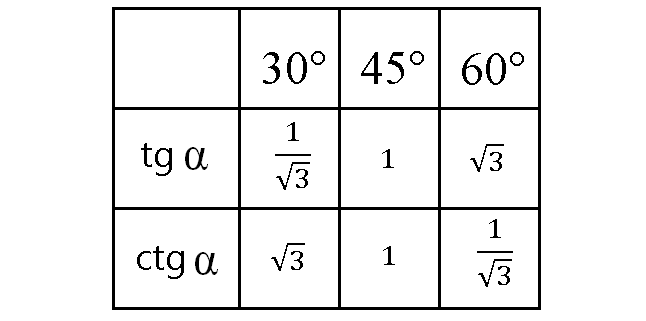
Этого достаточно, чтобы понять, что представляет из себя значение этих четырех тригонометрических функций для углов меньших 90°. В 10-11 классах понадобится умение быстро определять эти значения и для углов больше 90°, и для углов меньше нуля, да и измерять углы уже будут не в удобных градусах, а в радианах. Есть простой способ научиться этому, если, конечно, нет желания зубрить эту таблицу и еще очень многое другое.
