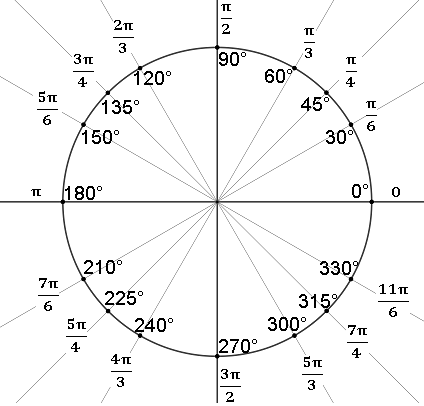
Радианы и градусы

Мало кто понимает, зачем углы иногда измеряют не в удобных и понятных градусах, а в радианах. Но чтоб понять, чем радианы лучше, нужно сначала узнать что это такое, а потом я расскажу что в них хорошего.

На самом деле измерение в градусах с математической точки зрения гораздо более противоестественно. Дело в том что, любая тригонометрическая функция (например, синус) — это все-таки математическая функция и иметь дело может только с числами, точно так же, как перед тем как вычислить квадратный корень из числа не нужно переводить число из одной единицы измерения в другую. А градус – это именно единица измерения, и это много чему мешает, особенно в высшей математике. Но сначала необходимо рассказать что такое число π (читается «пи»). Для этого начертим окружность и измерим ее диаметр.

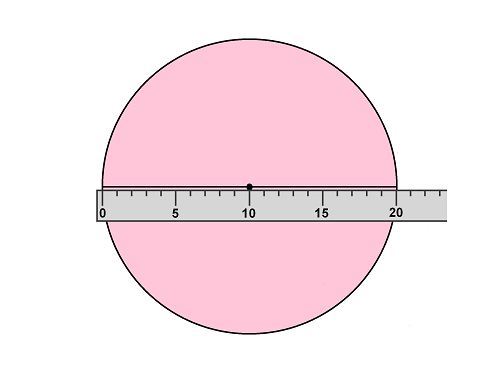
Диаметр равен 20 см. Затем загнем эту линейку и измерим всю длину этой же окружности.

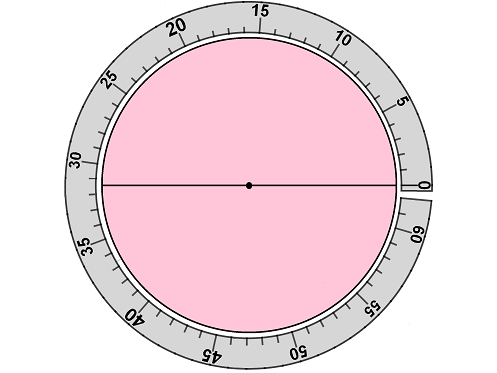
Длина окружности оказалась равной где-то 62,8 см. И если разделить длину окружности на длину диаметра этой же окружности, то получится приблизительно 3,14:

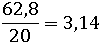
Это число приблизительно будет равно числу π, которое показывает во сколько раз точно длина окружности больше ее диаметра:

Если начертить окружность любого другого размера, и разделить окружность на диаметр, то получится примерно то же самое число 3,14. Абсолютно точно написать значение числа π невозможно, т.к. оно иррациональное. В виде числа его можно написать только приблизительно с разной степенью точности:

Цифры будут идти до бесконечности. Поэтому, когда имеют ввиду именно абсолютно точное значение этого числа, вместо 3,14 или 3,14159, пишут просто π.

Теперь возьмем единичную окружность (еще ее называют тригонометрической окружностью) с радиусом равным одному и с центром в начале координат.

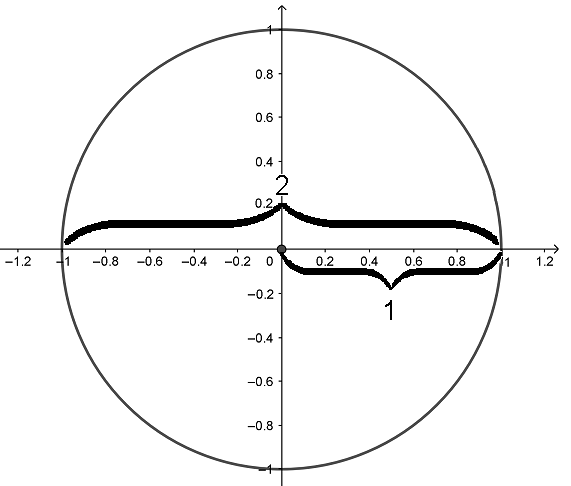
Радиус нашей единичной окружности равен одному, значит, ее диаметр равен двум. Тогда длина этой окружности будет равна:

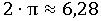
Потому что если умножить диаметр окружности на π, то получится длина этой окружности.

Теперь проведем луч AB так, чтобы длина красной дуги BC была равна 1. И тогда получившийся угол как раз будет равен одному радиану. То есть угол в радианах – это длина дуги этого угла на единичной окружности.

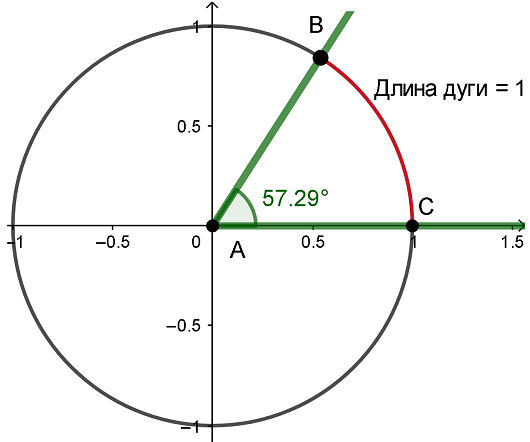
Если этот же угол, равный 1 радиану, измерить в градусах, то будет приблизительно 57,29 градусов:

Следовательно, если умножить на 2, то получится угол 2 радиана, который приблизительно будет равен 114,59°:

Но такие углы редко используются. Зато угол 30° используется часто, угол 30° на тригонометрической окружности образует дугу приблизительно равеную 0,52, значит:

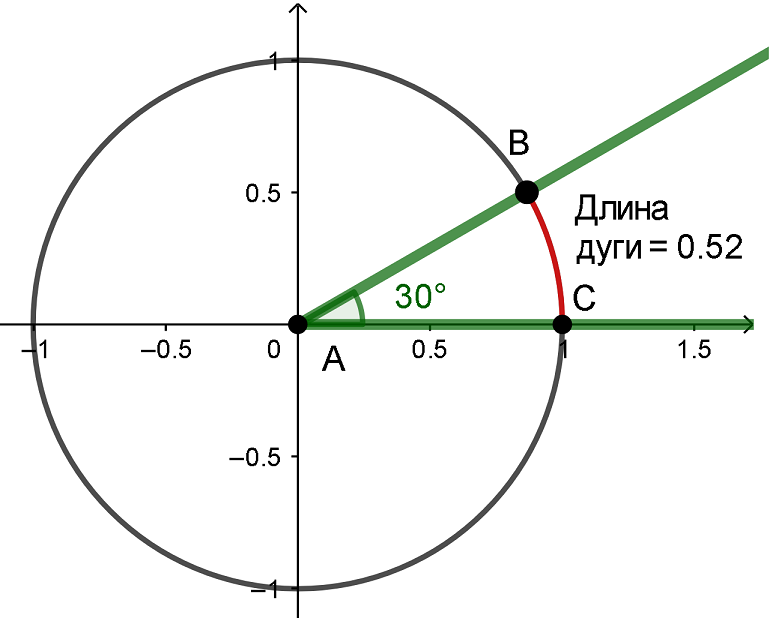
Это совсем неудобно, к тому же все результаты приближенные, а в математике нужна абсолютная точность. Подумаем, как можно все упростить и сделать точным, на следующем примере.

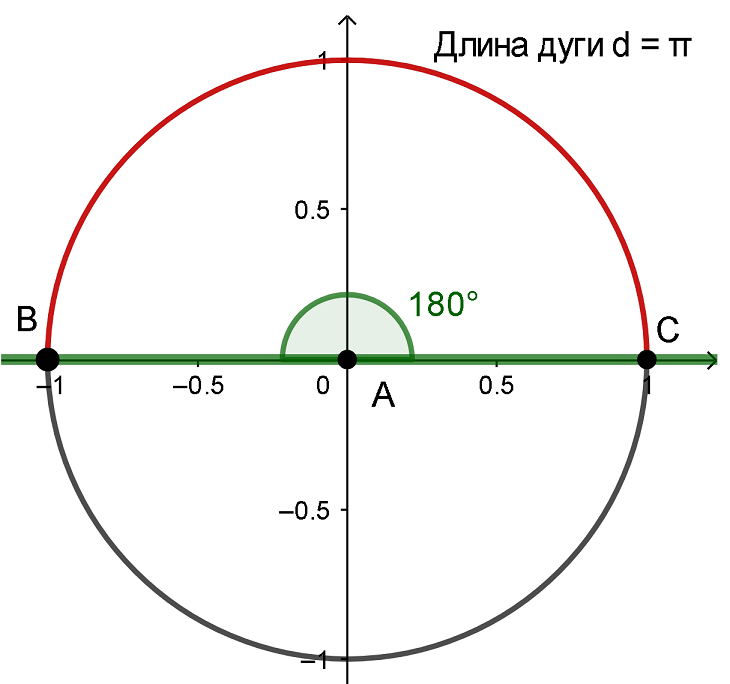
Нарисуем угол 180° на единичной окружности. Длина образовавшейся дуги равна углу в радианах. Очевидно, что длина такой дуги равна половине всей длины окружности, мы уже установили, что вся единичная окружность равна приблизительно 6,28, а точно — 2∙π. Значит, половина дуги будет равна приблизительно 3,14, а точно — π. В таком случае 180° = π радиан:

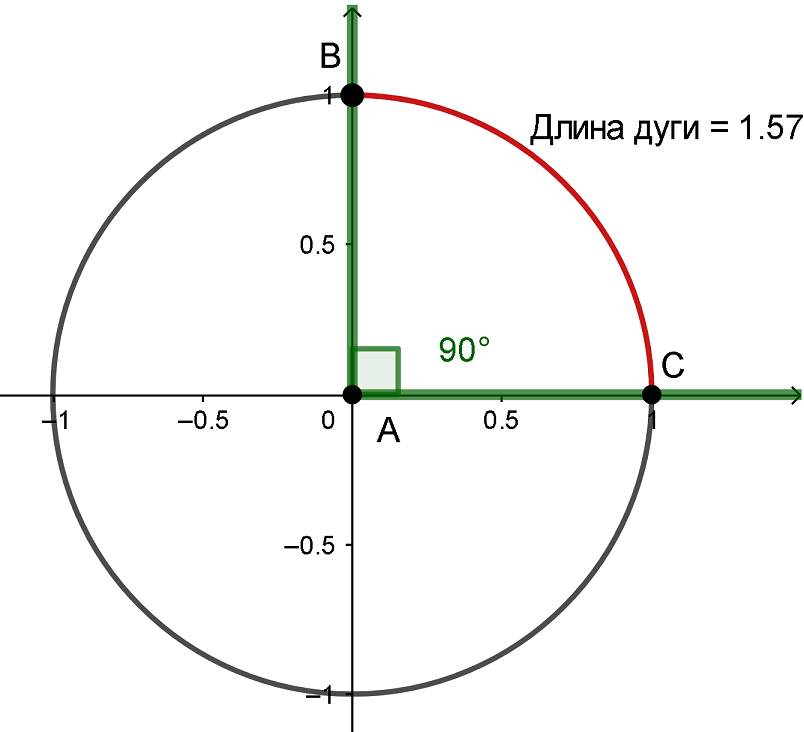
Рассуждая аналогично, переведем в радианы самый популярный угол: 90° в два раза меньше 180°, а 180° = π радиан. Выходит, 90° в радианах тоже в 2 раза меньше чем π, значит:

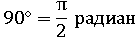
Приблизительно:

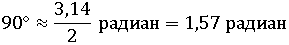
Так как 90° = 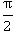радиан, то чтоб перевести в радианы 30°, надо 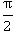разделить на 3:

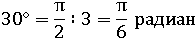
Приблизительно:

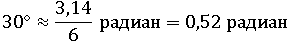
Чтоб перевести 150° в радианы, воспользуемся тем, что 30° = 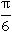, и умножим все на 5:

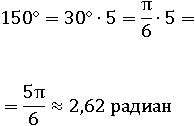
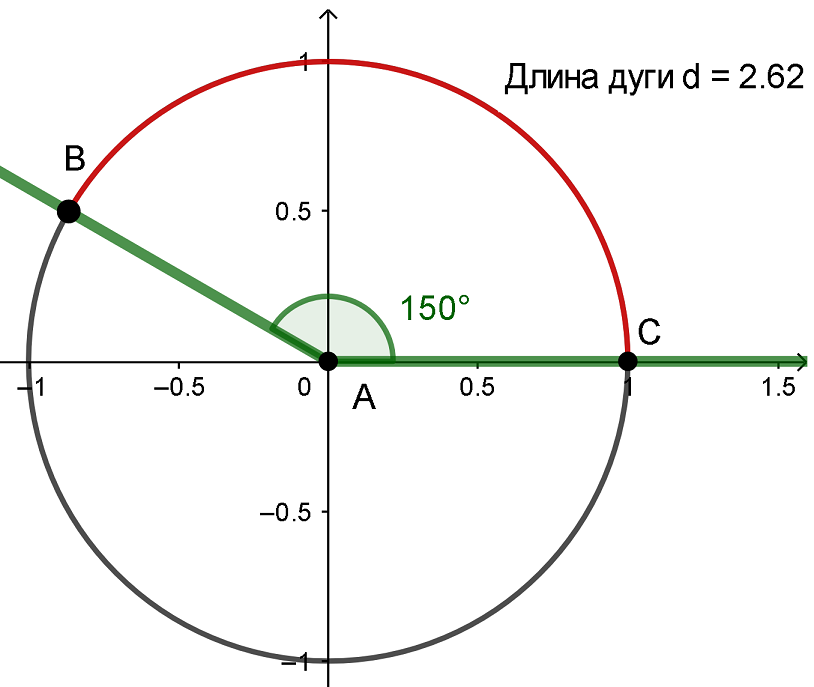
Связь между градусами и радианами довольно проста:

И чтоб перевести радианы в градусы, достаточно вместо π поставить 180°, посчитать и поставить знак градуса «°».

Переведем 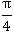в градусы:

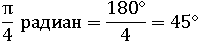
Приведем еще несколько примеров:

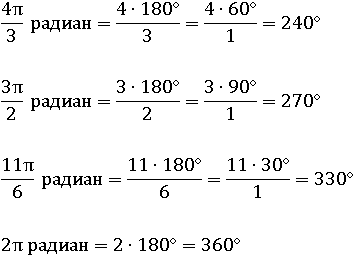
Чтобы перевести обратно из градусов в радианы, надо угол в градусах разделить на 180 и умножить на π:

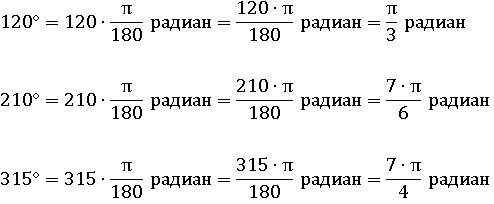
Благодаря радианам многие формулы стали выглядеть проще и естественней. Так, например, формула, по которой считали длину дуги в градусах, выглядит так:

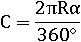
где R – радиус окружности, α – угол в градусах

И вот формула длины дуги через угол в радианах:

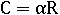
где R – радиус окружности, α – угол в радианах.

Попробуем применить последнюю формулу на следующей задаче.

Допустим, требуется найти длину синей дуги, которая является частью окружности с центром в точке A, с радиусом 4 (см. следующий рисунок). Известно, что угол A равен 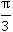радиан.

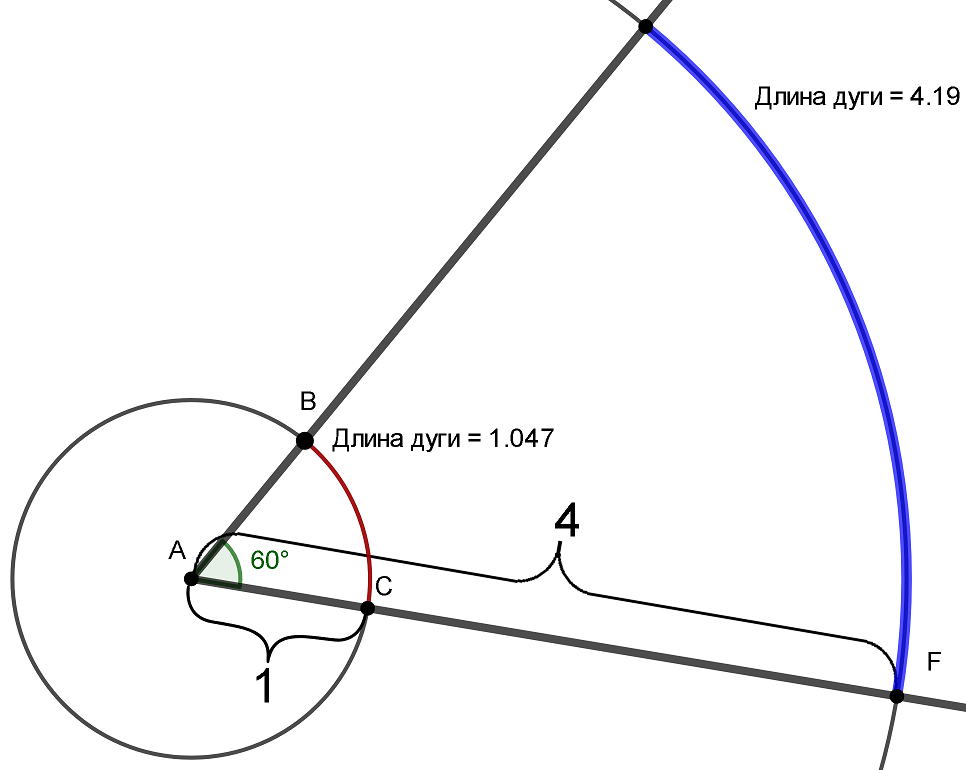
Начертим окружность с радиусом 1 с центром в точке A. длина красной дуги BC единичной окружности – это и есть угол A в радианах. Тогда длина красной дуги тоже будет равна 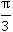. Радиус большей окружности в четыре раза больше радиуса единичной окружности, значит, и синяя дуга большей окружности в четыре раза больше красной дуги единичной. Осталось только умножить 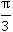на 4 и получить длину синей дуги :

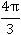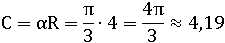
Таким образом, если воспринимать угол как длину дуги единичной окружности, сразу становится очевидным, что надо просто умножить величину угла в радианах на радиус R.

Есть еще одно очень полезное свойство радиана. Как нам уже известно из этой статьи, с помощью тригонометрической окружности можно приближенно определить синус и тангенс любого угла. И когда угол очень маленький, синус и тангенс угла практически не отличается от самого угла в радианах. На следующем рисунке угол A в радианах равен длине красной дуги BC, которая имеет почти такую же длину как зеленый отрезок, равный синусу угла A, и как синий отрезок, равный тангенсу угла A.

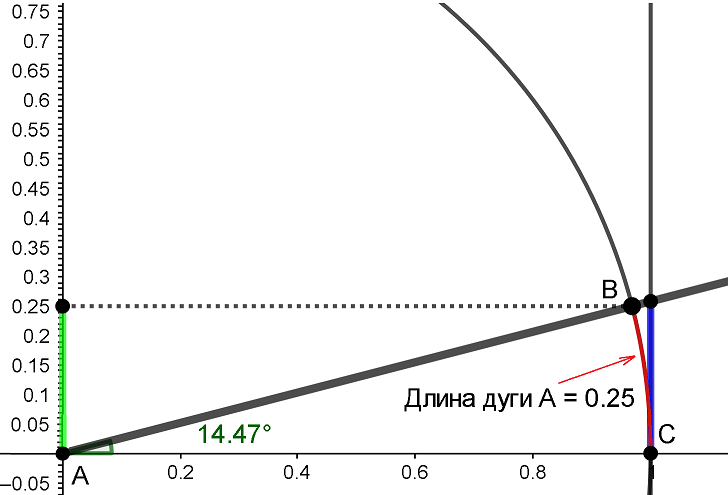
Так как длина дуги AB приблизительно равна 0,25, то получается, что синус 0,25 радиан и тангенс 0.25 радиан приблизительно равны 0.25. Причем по рисунку видно, что зеленый отрезок меньше красной дуги, а красная дуга меньше синего отрезка. Значит, sin 0,25 будет чуть меньше 0,25, а tg 0,25 - чуть больше 0,25.

Проверим это на калькуляторе.

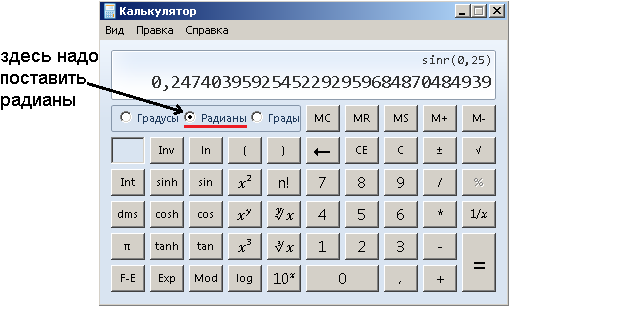
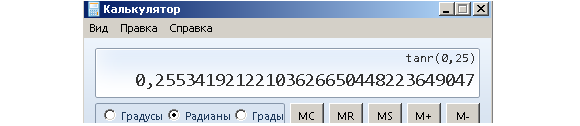
По этой причине при малых A можно sin A заменить на просто A. Это существенно упрощает многие расчеты.

Следовательно, при малых A:

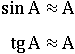
На следующем рисунке изображена единичная окужность со всеми школьными углами в градусах и радианах.

© Кирилл Морковкин & Машка Кулибякина