Примеры
Настало время закрепить все навыки раздела «степени и корни» и подробно разобрать другие примеры на эту тему, в том числе и более сложные чем обычно. Ниже представлены наиболее распространенные типы заданий:
Вынести множитель из-под знака корня
Пример № 1
Вынести множитель из-под знака корня:
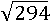
Решение.
Если немного присмотреться к числу под корнем, то можно заметить, что оно делится на 2, значит, оно равно произведению этих чисел:
269=2∙147
Еще 294 делится на 3:
269=3∙98
Следовательно, 294 делится и на 6:
269=6∙49
Тогда число под корнем можно заменить произведением этих чисел:
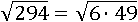
Первое свойство корня утверждает, что корень из произведения чисел равен произведению корней этих чисел:
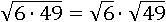
А корень из 49 равен семи:
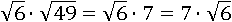
Больше вынести из-под корня ничего не получится.
Пример № 2
Вынести множитель из-под знака корня:
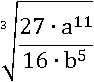
Решение.
Кубический корень прекрасно извлекается из чисел, которые являются кубами. Представим подкоренное выражение в следующем виде:
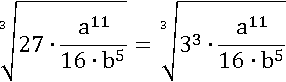
Под корнем получилось произведение 3 3 и дроби, применим первое свойство корня:
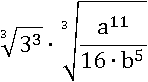
Кубический корень из 3 3 равен трем:
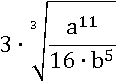
Из 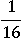 кубический корень удобно не извлекается, но удобно извлекается из
кубический корень удобно не извлекается, но удобно извлекается из 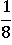 , тогда представим 16 в виде 8∙2, и вынесем таким же образом
, тогда представим 16 в виде 8∙2, и вынесем таким же образом 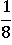 :
:
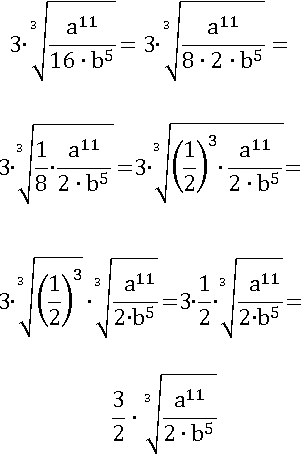
Проделаем то же самое и с a 11:
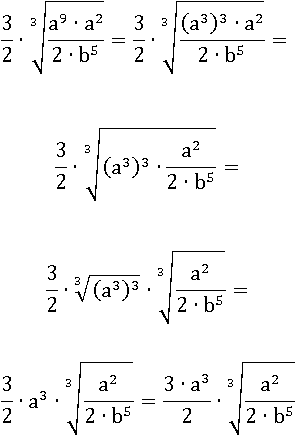
Осталось только вынести b 3:
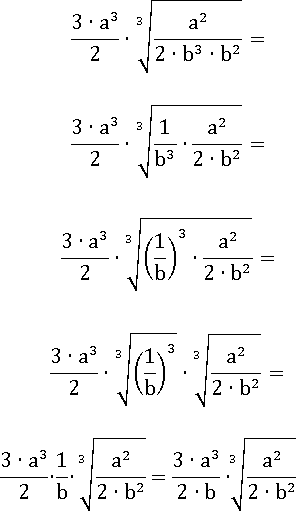
Этот способ простой, но долгий. Можно было бы все сделать быстрее:
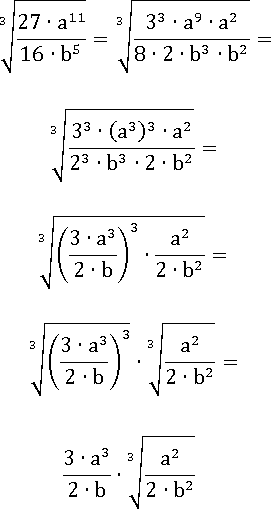
Сравните числа
Пример № 3
Сравните числа:

Решение.
Первый способ.
Чтоб сравнить два числовых выражения, совсем не обязательно вычислять их значения, часто достаточно представить эти выражения в каком-либо похожем виде так, чтобы они как можно меньше отличались друг от друга.
Попробуем сделать так, чтобы корень 2-й степени из шести тоже стал корнем 4-й степени, для этого нам понадобится пятое свойство корня:
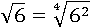
Число 6 2 под корнем можно заменить на 36:
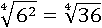
И теперь можно сравнивать уже эти числа:

Очевидно, что 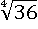 больше чем
больше чем 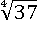 , т.к. чтобы получить число 37, нужно четырежды умножить на себя большее число, чем чтобы получить 36 (см. определение корня n-й степени), тогда и в изначальном виде первое число больше второго:
, т.к. чтобы получить число 37, нужно четырежды умножить на себя большее число, чем чтобы получить 36 (см. определение корня n-й степени), тогда и в изначальном виде первое число больше второго:
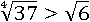
Второй способ.
Можно воспользоваться этой формулой, и заменить корни степенями в обоих выражениях:
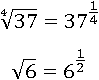
Изменим вид второму выражению с помощью третьего свойства степени:
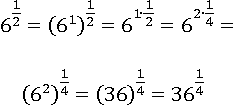
У обоих выражений стали одинаковые положительные показатели и их можно легко сравнить:
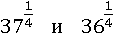
Первое число больше:
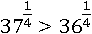
Значит, первое число было больше второго:
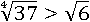
Но если бы степени были отрицательными, то больше было бы второе число.
Третий способ.
Оба выражения имеют значения явно превышающее единицу, значит, если оба выражения возвести в 4-ю степень, то большее останется большим, а меньшее – меньшим:
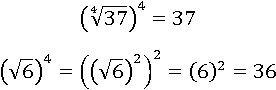
Первое число больше после возведения в степень, следовательно, оно было больше и до возведения:
37>36
Следовательно:
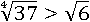
Четвертый способ.
Нам уже известно, что 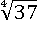 больше чем
больше чем 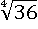 :
:
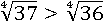
Но так как:
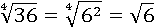
То получается следующее: 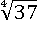 больше чем
больше чем 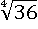 , который равен
, который равен 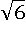 , следовательно,
, следовательно, 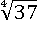 больше
больше 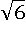 :
:
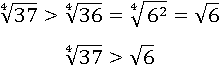
И приближенные значения обоих чисел показывают, что первое число больше:
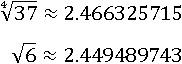
Пример № 4
Сравнить числа:
2300 3200
Решение.
Возвести 2 в трехсотую степень быстро не получится, 2 300 – очень большое число, состоящее из 91 цифры. Поэтому чтобы узнать, какое число больше, нужно их представить в более похожем друг на друга виде, используя третье свойство степени:
2300=2(3∙100)=(23)100=8100
3200=3(2∙100)=(32)100=9100
И уже очевидно, что:
8100 < 9100
Тогда:
2300 < 3200
Всё верно, число 3 200 состоит из 96-ти цифр – оно больше.
Пример № 5
Расположить в порядке возрастания:
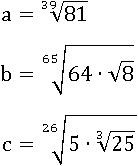
Решение.
Попытаемся привести числа к менее разнообразному виду, заменив корни степенями:
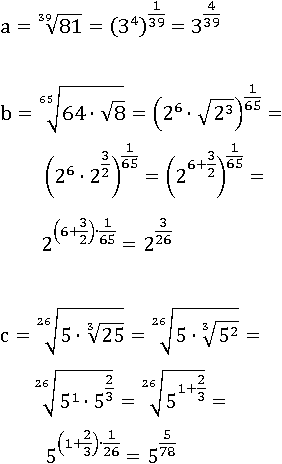
Домножим дроби в показателях чисел a и b, чтобы у всех них был знаменатель 78:
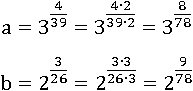
Показатели у всех чисел стали более похожими и их даже можно легко сравнить, но основания (числа 2, 3 и 5) остались разными. Все три основания больше единицы и показатели у них положительные, следовательно, если все числа возвести в 78-ю степень, большее число останется большим, а меньшее меньшим и их все еще можно будет сравнивать:
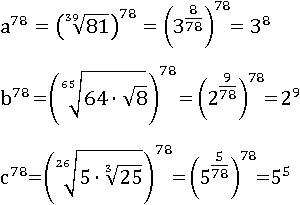
Чтобы не вычислять 3 8 и 5 5, разделим a 78 на c 78:
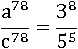
Приведем результат деления к такому виду, чтоб можно было с уверенностью утверждать больше он одного или нет. Если получится число больше единицы, то a 78 больше c 78, в противном случае – наоборот:
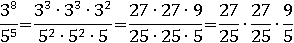
Очевидно, что каждая из дробей больше единицы, тогда и всё произведение дробей больше единицы, значит, a 78 больше c 78, следовательно, и a больше c.
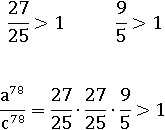
Сравним тем же способом числа b 78 и c 78:
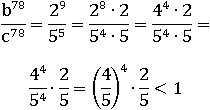
Число b 78 оказалось меньше c 78, из чего следует, что b меньше c. Таким образом, выходит: a больше c, а b меньше c; значит, самое маленькое число – b, среднее – c, а самое большое – a:
b<c<a
Разложить на множители
Пример № 6
Разложить на множители:
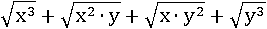
Решение.
Чтобы разложить на множители выражение, его надо представить в виде произведения каких-нибудь других выражений. Для этого нужно попытаться заметить что-нибудь общее у некоторых слагаемых. Будет легче, если, используя свойства корня, представить в виде произведения каждое слагаемое:
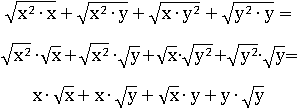
В первом и третьем слагаемом есть одинаковый множитель 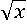 , во втором и четвертом –
, во втором и четвертом – 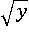 , поставим их ближе друг к другу:
, поставим их ближе друг к другу:
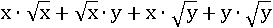
Появилась возможность вынести общий множитель за скобку. Так и сделаем:
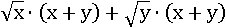
Сумма (x+y) – тоже общий множитель, вынесем и его за скобку:
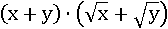
Теперь первоначальное выражение разложено на произведение двух множителей. Проверим равносильность, пусть x=4, y=9:
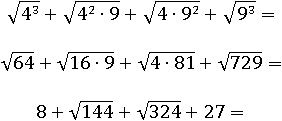
8+12+18+27=65
В разложенном на множителе виде выражение тоже равно 65:
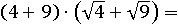
13∙(2+3)=13∙5=65
Пример № 7
Разложить на множители:
4∙a4+81∙b4
Решение.
Оба слагаемых в сумме являются квадратами чисел 2∙a2 и 9∙b2:
(2∙a2)2+(9∙b2)2
Но не хватает удвоенного произведения этих чисел, чтобы можно было выделить полный квадрат. Если мы добавим удвоенное произведение, то число изменится и произойдет нарушение равносильности, а это грубая ошибка. Но если добавить удвоенное произведение и опять отнять его, то ничего не изменится:
(2∙a2)2 + (9∙b2)2 + 2∙(2∙a2)∙(9∙b2) − 2∙(2∙a2)∙(9∙b2)
Переставим:
(2∙a2)2 + 2∙(2∙a2)∙(9∙b2) + (9∙b2)2 − 2∙(2∙a2)∙(9∙b2)
Первые три слагаемых можно представить как квадрат суммы:
(2∙a2 + 9∙b2)2 − 2∙(2∙a2)∙(9∙b2)
Преобразуем второй член:
(2∙a2 + 9∙b2)2 − 2∙2∙9∙a2∙b2 =
(2∙a2 + 9∙b2)2 − 36∙a2∙b2 =
(2∙a2 + 9∙b2)2 − 62∙a2∙b2 =
(2∙a2 + 9∙b2)2 − (6∙a∙b)2
Получился квадрат одного выражения, от которого отнимается квадрат другого, значит, можно применить формулу сокращенного умножения разность квадратов:
((2∙a2 + 9∙b2) + (6∙a∙b))∙((2∙a2 + 9∙b2) − (6∙a∙b)) =
(2∙a2 + 9∙b2 + 6∙a∙b)∙(2∙a2 + 9 ∙ b2 − 6∙a∙b)
Проверим равносильность на числах, пусть a=5, b=2:
4∙a4 + 81∙b4 = 4∙54 + 81∙24 =
4∙625 + 81∙16 = 2500 + 1296 = 3796
И подставим эти же числа в разложенное на множители выражение:
(2∙a2 + 9∙b2 + 6∙a∙b)∙(2∙a2 + 9∙b2 − 6∙a∙b) =
(2∙52 + 9∙22 + 6∙5∙2)∙(2∙52 + 9∙22 − 6∙5∙2) =
(2∙25 + 9∙4 + 60)∙(2∙25 + 9∙4 − 60) =
(50 + 36 + 60) ∙ (50 + 36 − 60) = 146∙26 = 3796
Упростить
Пример № 8
Упростить:
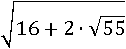
Решение.
Среди свойств корня и свойств степени нет ни одного, которое может преобразовать выражение 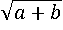 в что-то похожее на
в что-то похожее на 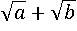 . Зато можно попробовать избавиться от внешнего корня, для этого надо, чтобы подкоренное выражение представляло из себя квадрат какого-нибудь числа. Это получится сделать, если представить подкоренное выражение в виде суммы квадратов двух чисел и удвоенного произведения этих же чисел, затем применить квадрат суммы. Такое преобразование называется выделением полного квадрата.
. Зато можно попробовать избавиться от внешнего корня, для этого надо, чтобы подкоренное выражение представляло из себя квадрат какого-нибудь числа. Это получится сделать, если представить подкоренное выражение в виде суммы квадратов двух чисел и удвоенного произведения этих же чисел, затем применить квадрат суммы. Такое преобразование называется выделением полного квадрата.
Число 16 заменим на 11+5, а 55 на 11∙5:
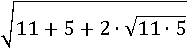
Переместим 5 в конец и разделим по разным корням произведение 11∙5:
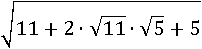
Представим 11 и 5 в виде квадратов:
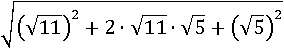
Теперь можно воспользоваться этой формулой сокращенного умножения, потому что под корнем получилось: квадрат первого числа, квадрат второго числа и удвоенное произведение первого и второго чисел, который равен квадрату суммы первого и второго чисел.
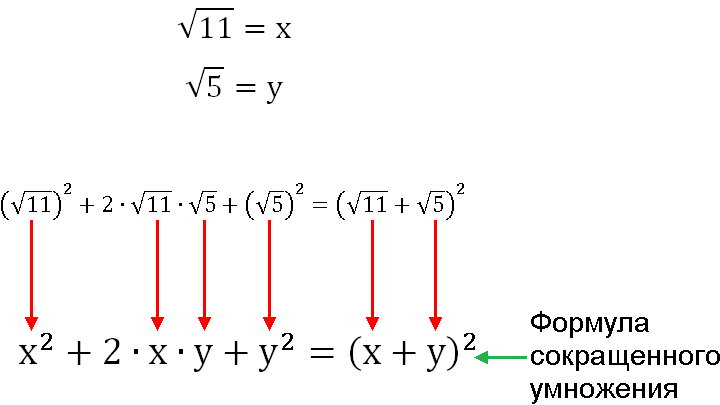
В таком случае можно заменить всё подкоренное выражение на более удобное, из которого можно легко извлечь корень:
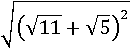
По определению квадратного корня данное выражение равно:
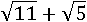
Приближенные значения исходного и упрощенного выражений равны:
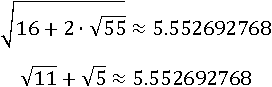
Пример № 9
Упростить:
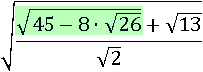
Решение.
Здесь следует сначала попытаться извлечь корень, выделенный таким зеленым цветом, тем же способом как в предыдущем примере – через выделение полного квадрата. Как правило, в таких случаях удвоенным произведением в подкоренном выражении является слагаемое содержащее корень, следовательно, в данном примере вероятнее всего удвоенным произведением будет 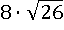 , значит, просто произведением (не удвоенным) этих чисел является
, значит, просто произведением (не удвоенным) этих чисел является 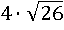 . Подумаем, какие это могут быть числа. Представим число
. Подумаем, какие это могут быть числа. Представим число 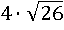 в таком виде:
в таком виде:
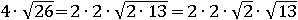
Выходит, что искомой парой чисел, произведение, которых равно 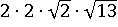 , могут быть:
, могут быть:
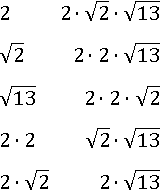
Теперь нужно выбрать какую-нибудь одну пару из этих пяти. Подходящим вариантом будет тот, в котором сумма квадратов обоих чисел из пары равна 45. Мы можем вычислить сумму квадратов каждой пары:
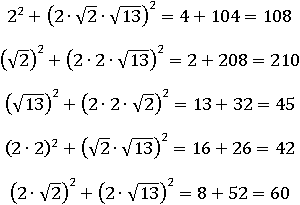
Можно вычислять каждый вариант по порядку пока не получится 45, но если присмотреться к исходному выражению, то можно заметить, что там уже есть 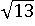 . Наверное, тот, кто придумывал этот пример (то есть я) поместил
. Наверное, тот, кто придумывал этот пример (то есть я) поместил 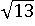 туда не просто так, а чтобы он потом сократился с другим
туда не просто так, а чтобы он потом сократился с другим 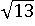 ? И число 26 почему-то тоже делится на 13. Всё это – намеки, указывающие, по какому пути следует идти. Чем сложнее задача, тем больше таких подсказок, значит, можно сразу начать проверку третьей пары – именно в ней есть
? И число 26 почему-то тоже делится на 13. Всё это – намеки, указывающие, по какому пути следует идти. Чем сложнее задача, тем больше таких подсказок, значит, можно сразу начать проверку третьей пары – именно в ней есть 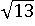 , и не тратить время на остальные.
, и не тратить время на остальные.
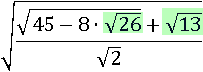
Подходит третья пара, тогда это подкоренное выражение можно представить в виде квадрата числа:
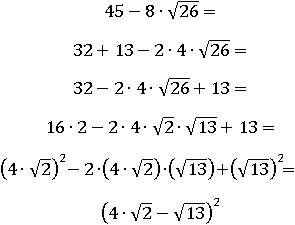
Дальше можно было бы заменить 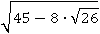 на
на 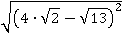 и извлекать корень, но дело в том что:
и извлекать корень, но дело в том что:
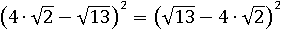
Причина этого в том, что числа под квадратом равны по модулю, но противоположны по знаку:
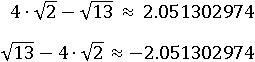
А так как число в четной степени всегда равно неотрицательному числу, то и квадраты этих чисел равны:
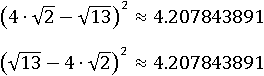
Но так как определение квадратного корня говорит, что корнем из числа называется именно неотрицательное число, то выбирать следует первый вариант:
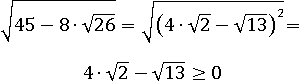
Тогда первоначальное выражение равносильно следующему:
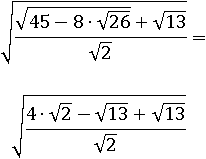
И действительно 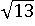 сокращается, затем и
сокращается, затем и 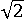 :
:
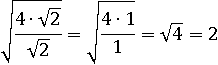
Получается, что вся эта махина – просто усложненное число 2:
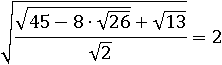
Пример № 10
Упростить выражение, считая, что все переменные принимают только положительные значения:
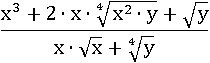
Решение.
Первый способ.
Должно быть сразу заметно, что здесь нужно будет применить формулу квадрат суммы, но сначала нужно подготовить это выражение, чтобы оно удовлетворяло всем условиям этой формулы. Для более удобного восприятия этого выражения заменим все корни соответствующими степенями по этой формуле:
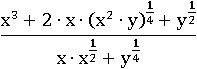
Раскроем скобки в числителе по четвертому свойству степени:
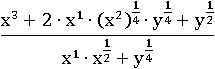
Оставшуюся скобку раскроем с помощью третьего свойства степени, а в знаменателе пока сложим показатели по первому свойству степени:
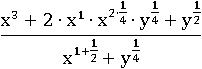
В числителе умножим 2 на 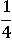 , в знаменателе сложим 1 и
, в знаменателе сложим 1 и 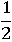 :
:
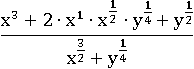
Опять применим первое свойство степени:
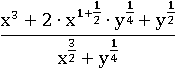
Наконец сложим дробь с единицей в показателе икса:
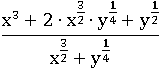
Представим тройку в показателе x как произведение 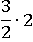 и
и 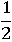 в показателе y как
в показателе y как 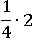 :
:
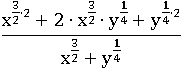
Применим третье свойство степени:
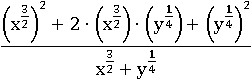
Теперь у нас появились квадраты первого и второго чисел и удвоенное произведение тех же самых чисел (в точности как в квадрате суммы). Если бы этого не получилось, то пришлось бы начинать все заново и искать другие пути решения, поэтому надо уметь видеть это заранее. Применим квадрат суммы:
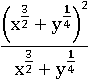
Квадрат числа в скобке равносилен умножению этого числа на само себя:
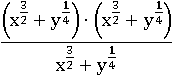
Получилась дробь, в которой весь числитель и весь знаменатель умножается на одно и то же число, то есть дробь полностью пригодная для применения основного свойства дроби, значит, можно сократить:
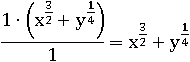
В сущности говоря, ответ уже готов, но если надо, то можно вернуть назад корни:
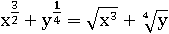
Второй способ.
Можно упростить выражение, не переходя от корней к степеням:
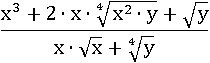
Применим первое свойство корня к будущему удвоенному произведению:
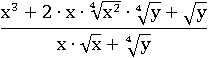
Поменяем x на 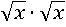 в двух местах:
в двух местах:
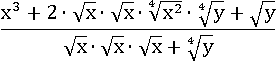
Извлечём корень 4-й степени из x 2
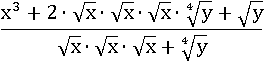
Применив первое свойство, занесем все x под один квадратный корень:
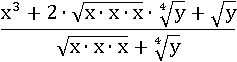
Перейдем от трехкратного умножения x к третьей степени:
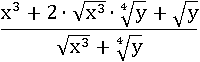
Если извлечь квадратный корень и назад возвести в квадрат неотрицательное число, то значение выражения не изменится, зато появятся квадраты нужные для квадрата суммы:
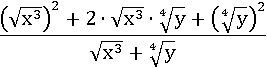
Теперь можно применить квадрат суммы:
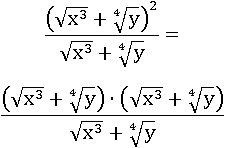
По условию все переменные принимают только положительные значения, значит, можно сократить и равносильность не пострадает:
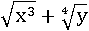
Получился тот же результат как и в прошлый раз.
Пример № 11
Упростить выражение, считая, что все переменные принимают только положительные значения:
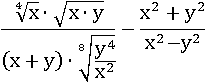
Решение.
Здесь лучше сразу перейти к степеням:
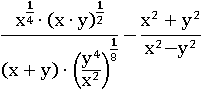
Раскроем все скобки с помощью четвертого и пятого свойств степени:
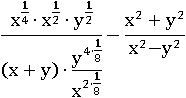
Умножим показатели в знаменателе первой дроби:
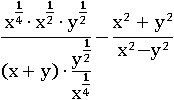
Далее придется складывать много дробей в показателях, это проще будет делать, если заменить все дроби в показателях на десятичные:
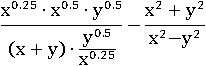
Воспользуемся основным свойством дроби – домножим первую дробь на x 0.25, чтобы сократить дробь в знаменателе:
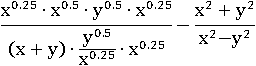
Теперь в знаменателе первой дроби y 0.5 делится на x 0.25 и опять умножается на x 0.25, от этого y 0.5 не изменяется, значит, можно убрать оба x 0.25:
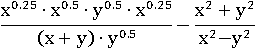
Домножим первую дробь на y −0.5:
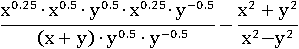
В числителе переставим множители для удобства:
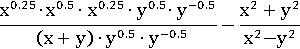
В первой дроби сложим все степени у x и y, воспользовавшись первым свойством степени:
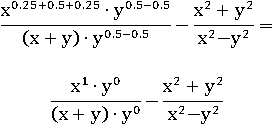
Любое число (кроме нуля) в нулевой степени равно единице, а умножение на один ничего не меняет – уберем все x 0 и y 0:
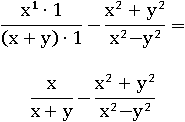
При сложении этих дробей всё выражение может упроститься, а для сложения дробей необходим одинаковый знаменатель; тогда вспомним формулу сокращенного умножения, которая называется разность квадратов и применим ее к знаменателю второй дроби – это самый простой путь для приведения таких дробей к одному знаменателю:
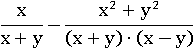
И уже видно, что, если домножить первую дробь на x−y, то знаменатели станут одинаковыми:
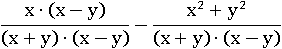
Можно сложить дроби:
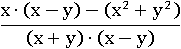
Раскроем все скобки в числителе:
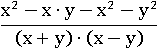
Сократим x2 и −x2 в числителе:
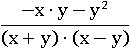
Вынесем за скобку −y:
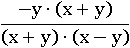
По условию x и y – положительные числа, следовательно, x+y не равно нулю, и можно сократить на x+y:
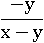
Умножим числитель и знаменатель на −1 и раскроем скобку, чтоб выражение было еще компактнее:
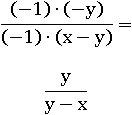
Это упрощенное выражение равносильно первоначальному при всех положительных x и y:
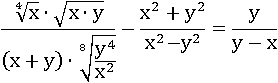
Допустим x=16, а y=9, тогда первоначальное выражение будет равно 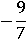 :
:
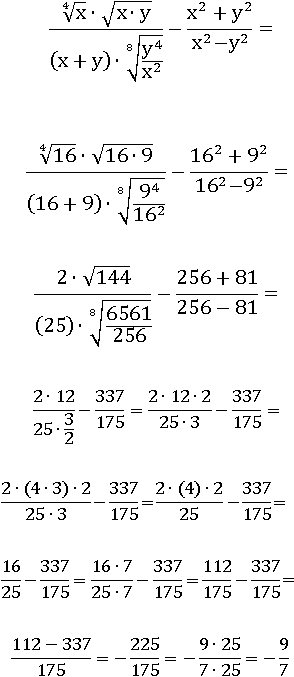
Упрощенное выражение при x=16, а y=9 тоже будет равно 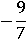 :
: