Числовая ось. Промежуток. Модуль.
- Числовая ось
- Числовые промежутки
- Модуль действительного числа
- Геометрический смысл модуля
- Свойства модуля
Числовая ось
Возьмем вот такую прямую бесконечную в обе стороны. Её называют числовой осью, числовой прямой или координатной прямой.

Расположим на ней по порядку через равные промежутки все целые числа так, чтобы они возрастали при перемещении по прямой слева направо (туда показывает стрелка на оси). Естественно, целиком бесконечную прямую со всеми целыми числами разместить на ограниченном рисунке невозможно, но при этом следует понимать, что все они там есть, потому что прямая бесконечная – всем целым числам хватит места.

Но между каждыми соседними целыми числами еще полно места, тогда ровно между числом 1 и числом 2 поместим рациональное число 1.5.

Можно разместить на этой же оси еще некоторые рациональные числа: очевидно, что ровно посередине между 1 и 1.5 можно добавить еще рациональное число 1.25. А между 1.5 и 2 – число 1.75 и т.д.

Так только между числами 1 и 2 можно поставить бесконечное количество рациональных чисел. Обозначить каждое на рисунке не получится, но каждое из них точно там присутствует.

И вообще можно разместить все рациональные числа, но отметить на числовой прямой удастся тоже только некоторые из них.
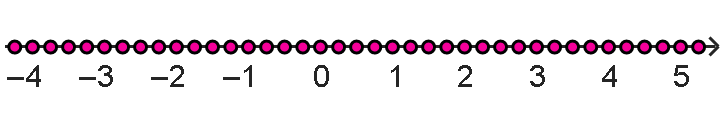
Только кажется, что на числовой прямой совсем не осталось места. Иррациональные числа не является ни рациональными, ни целыми, значит, они не займут чужого места, уже занятого рациональными числами. Расположим на оси по порядку все иррациональные числа. И только тогда свободного места на числовой прямой уже совсем не останется – каждая точка будет обязательно занята каким-нибудь числом, а для каждого действительного числа точно найдется своя одна точка на оси.
Такая прямая со всеми действительными числами называется числовой прямой.

Числовая ось – это геометрическая модель всех действительных чисел, она незаменима при решении многих математических задач. На числовой прямой видны некоторые закономерности с геометрической точки зрения: все положительные числа находятся правее нуля, а все отрицательные левее нуля; большие числа всегда правее меньших; чем больше число, тем правее оно расположено.
Числовые промежутки
Во многих задачах требуется указывать множество чисел, при которых выражение или функция принимает те или иные значения или обладает какими-нибудь свойствами. Таких чисел может быть бесконечно много и просто перечислить все их невозможно. Поэтому удобнее не перечислять их, а указывать лишь границы, в пределах которых находится это множество чисел.
Например, чтобы обозначить множество всех действительных чисел от 1 до 2 нужно в квадратных скобках указать первое самое маленькое число из этого множества, затем через точку с запятой – самое большое число из этого множества:
[1; 2]
Квадратные скобки в этом промежутке означают, что само число 1 и само число 2 тоже входят в это множество чисел. Такой промежуток с двумя квадратными скобками называется отрезком. В этот промежуток входят такие числа как:
![Числа из [1; 2] 1;1.03; 3/2; 1.98;2](img7/f010.png)
Каждое из этих чисел больше или равно одному и меньше или равно двум. Разумеется, это не все числа из этого промежутка, а только некоторые из них, поскольку действительных чисел от одного до двух бесконечно.
Множество чисел от одного до двух можно изобразить на числовой оси: каждое число, которое находится в заштрихованной области, принадлежит множеству [1; 2]. Жирные закрашенные точки 1 и 2 означают, что числа 1 и 2 входят в этот промежуток.
![[1; 2] на оси Отезок [1; 2]](img7/080.png)
Если нужно указать промежуток от одного до двух так, чтобы туда не входили числа 1 и 2, то вместо квадратных скобок следует поставить круглые:
(1; 2)
Промежуток с двумя круглыми скобками называется интервалом. В промежуток (1; 2) входят те же числа, что и в отрезок [1; 2] кроме 1 и 2. Расположим по возрастанию некоторые числа из этого интервала:
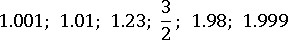
На числовой прямой интервал (1; 2) изображают так, чтобы показать, что числа 1 и 2 не входят в этот промежуток, для этого точки 1 и 2 помечают незакрашенными кружочками, такие точки называются выколотыми.

Следует заметить, что в любом интервале нет самого большого и самого маленького числа. Какое самое большое число в интервале (1; 2), если числа 2 в нем нет? К числу 2 можно бесконечно приближаться и так никогда не дойти до самого большого в интервале:
1.9999; 1.99999; 1.999999; 1.9999999; 1.99999999...
Если в промежуток от одного до двух надо внести только число 1, а число 2 оставить за его пределами, то первую скобку рядом с единицей делают квадратной, а вторую – круглой:
[1; 2)
Этот промежуток называется полуинтервалом. В него входят все действительные числа, от единицы до двух, включая единицу, но не включая два, например, такие:
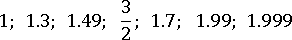
Множество чисел [1; 2) на числовой оси изображают с закрашенной точкой 1 и незакрашенной точкой 2 в виде маленького кружочка.

Также можно задать полуинтервал, в котором нет единицы, но есть два – для этого достаточно рядом с единицей поставить круглую скобку, а рядом с двойкой – квадратную:
(1; 2]
На числовой оси промежуток (1; 2] будет с незакрашенной точкой 1 и закрашенной точкой 2.
![(1; 2] на оси Промежуток (1; 2]](img7/110.png)
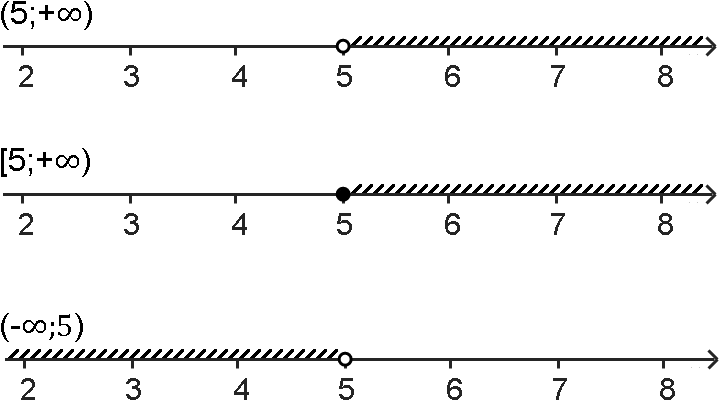
Промежуток не обязательно должен быть ограничен с двух сторон – снизу и сверху. Иногда требуется задать множество всех чисел, которые только больше пяти и никаких ограничений сверху не имеют. Такое множество можно задать промежутком от пяти до плюс бесконечности:
(5; +∞)
Бесконечность обозначают символом ∞. Рядом с плюс или минус бесконечностью всегда надо ставить только круглую скобку.
В промежуток (5; +∞) входят все числа, которые больше пяти не включая самого числа пять, вот некоторые из них:
5.001; 5.02; 5.1; 9.4; 101; 1934.5; 4064.734; 735361698; ...
Но пять можно включить в промежуток, заменив первую скобку на квадратную:
[5; +∞)
Множество чисел, которые меньше пяти можно обозначить промежутком от минус бесконечности до пяти:
(−∞; 5)
В него будут входить все отрицательные числа и положительные, которые меньше пяти. Например, такие:
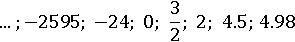
Промежутки, содержащие одну плюс или минус бесконечность, называют лучом. На числовой оси луч изображают в виде промежутка с одним концом, уходящим в бесконечность.
Множество всех действительных чисел, не ограниченное ни сверху, ни снизу, обозначают промежутком от минус бесконечности до плюс бесконечности:
(−∞; +∞)

В этот промежуток входят абсолютно все действительные числа.
Часто приходится задавать множество чисел, состоящее из нескольких разных промежутков, например таких:
[4.3; 5) (6; 8.5] (−1; 3)
В этом случае промежутки расставляют в порядке возрастания чисел, которые в него входят. Любое число из промежутка (−1; 3) меньше любого другого числа из остальных промежутков, значит, это промежуток будет стоять первым. Любое число из промежутка (6; 8.5] больше любого другого числа из остальных промежутков, значит, этот промежуток будет стоять последним. В середине будет промежуток [4.3; 5):
(−1; 3) [4.3; 5) (6; 8.5]
Затем между каждыми двумя промежутками ставят такой знак ∪ объединения:
(−1; 3)∪[4.3; 5)∪(6; 8.5]
На числовой прямой это множество будет выглядеть так.
![(−1; 3)∪[4.3; 5)∪(6; 8.5] (−1; 3)∪[4.3; 5)∪(6; 8.5]](img7/140.png)
Чтобы убрать какое-нибудь число из середины промежутка, удобно использовать объединение. Например, исключим ноль из этого промежутка:
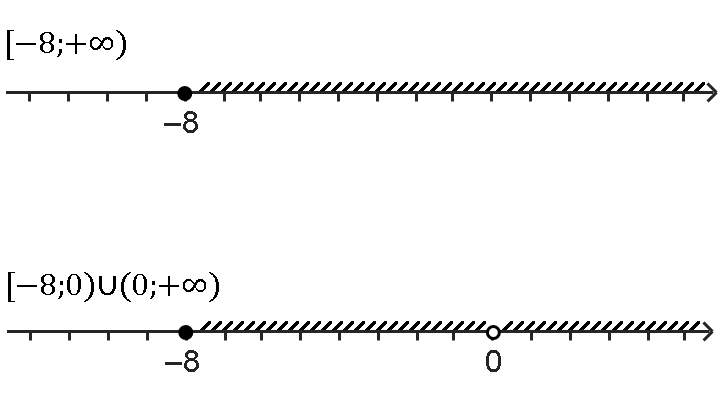
[−8; +∞)
Промежуток [−8; +∞) равен объединению этих промежутков:
[−8; 0)∪[0; +∞)
Ноль по-прежнему входит в это объединение, но если поменять одну квадратную скобку на круглую, то нуля там уже не будет:
[−8; 0)∪(0; +∞)
Теперь в этом объединении содержатся те же самые числа, что и в промежутке [−8; +∞) кроме нуля. На числовой оси точку ноль следует обозначить незакрашенным кружком как не входящую в это множество.
Модуль действительного числа
Модуль числа x обозначается так:
|x|
Модуль действительного числа x равен числу x, если x больше нуля или равен ему. Например, число 3 больше нуля, значит, модуль этого числа равен трем:
|3|=3
Число 0.2 тоже больше нуля, значит, модуль этого числа равен 0.2:
|0.2|=0.2
Модуль одного равен одному, потому что один больше нуля:
|1|=1
Ноль равен нулю, значит модуль нуля – ноль:
|0|=0
Модуль действительного числа x равен числу −x, если x меньше нуля. Например, число −7 – меньше нуля, значит, его модуль равен семи:
|−7|=−(−7)=7
Число −2.1 меньше нуля, следовательно, модуль этого числа равен 2.1:
|−2.1|=−(−2.1)=2.1
Получается, что если действительное число является неотрицательным, то модуль его не изменит. Если действительное число отрицательное, то модуль сделает его положительным:
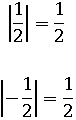
|17|=17
|−14.9|=14.9
Обычно определение модулю дают с помощью такой формулы:
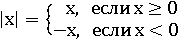
Подобную запись надо понимать следующим образом. После знака равно в этой формуле есть два варианта ее продолжения, первый вариант – для случая, когда x больше нуля или равен ему:
|x|=x, если x≥0
Второй вариант формулы – для случая, когда x меньше нуля:
|x|=−x, если x<0
Пример
Упростить:
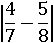
Решение.
Не всегда сразу понятно больше или меньше нуля число под знаком модуля. Значит, сначала нужно упростить выражение под модулем, поэтому отнимем одну дробь от другой.
Приведем к общему знаменателю:
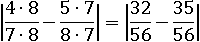
И отнимем дроби:
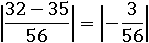
Теперь очевидно, что под модулем отрицательное число, следовательно модуль этого числа то же самое число, только положительное:
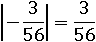
Геометрический смысл модуля
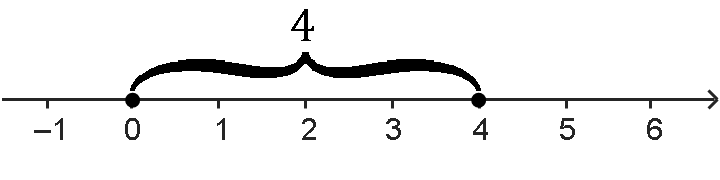
У модуля числа есть свой геометрический смысл: модуль числа x равен расстоянию от точки ноль до числа x на числовой прямой. Например, модуль числа 4 равен четырем:
|4|=4
Значит, и расстояние между числами 0 и 4 на числовой оси равно четырем.
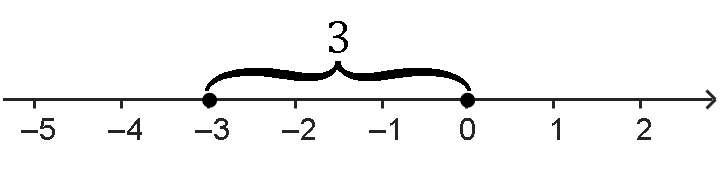
Также можно вычислить расстояние от числа −3 до нуля на оси:
|−3|=3
Расстояние r между любыми двумя точками a и b на числовой прямой можно вычислить по такой формуле:
r=|a−b|
Или по такой – результат будет одинаковым:
r=|b−a|
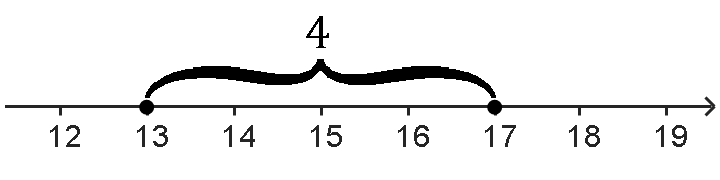
Например, расстояние на числовой прямой между числами 13 и 17 равно четырем:
r=|17−13|=|4|=4
Хотя можно было посчитать и так:
r=|13−17|=|−4|=4
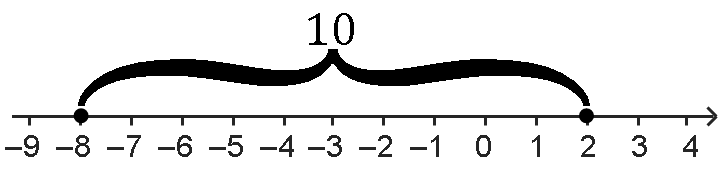
Расстояние между числами −8 и 2:
r=|−8−2|=|−10|=10
Если переставить, то получится тоже 10:
r=|2−(−8)|=|2+8|=|10|=10
Свойства модуля
У модуля есть некоторые свойства, они довольно просты и логичны.
Свойства модуля
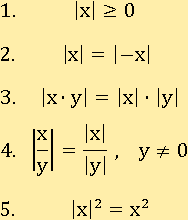
Догадаться, что такие свойства у модуля есть легко – все они прямо вытекают из определения, поэтому лишь немного затронем каждое из них.
В первом свойстве всё просто: очевидно, что модуль любого числа является неотрицательным числом. Например:
|4.7|≥0
|−6.3|≥0
Второе свойство утверждает, что если число под модулем умножить на −1, то значение модуля этого числа не поменяется, и не важно, положительным было это число или отрицательным:
|9|=|−9|=9
|−7|=|−(−7)|=7
Третье свойство говорит, что модуль произведения любых чисел всегда будет равен произведению модулей этих чисел:
|3∙5|=|3|∙|5|=3∙5=15
|(−3)∙5|=|−3|∙|5|=3∙5=15
Аналогичная будет ситуация и с делением в четвертом свойстве:
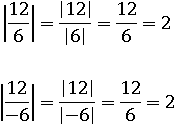
В последнем свойстве запись |x|2=x2 имеет тот же смысл, что и это выражение:
|x|∙|x|=x∙x
Если умножить друг на друга два одинаковых действительных числа x, то получиться может только либо положительное число, либо ноль; следовательно, неважно умножать x на x или |x| на |x| результат умножения будет одинаковым:
|2|∙|2|=2∙2=4
|−2|∙|−2|=(−2)∙(−2)=4