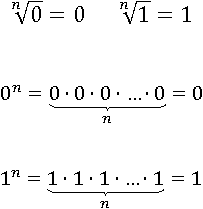Корень n-й (любой) степени из действительного числа
Есть в математике такая операция – возведение числа в степень с натуральным показателем. Такая операция позволяет из числа 5 получить его квадрат равный 25, а из числа 3 четвертую степень этого числа равную 81:
52=5∙5=25
34=3∙3∙3∙3=9∙9=81
Но довольно часто возникает необходимость производить обратную операцию, например, выяснять какое число в квадрате будет равно 25. Мы уже изучали операцию обратную возведению в квадрат – извлечение квадратного корня.
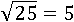
Таким образом, есть прямая операция, позволяющая из числа 5 получить его квадрат 25; и обратная операция, с помощью которой можно из 25 назад получить число 5:
52=25
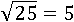
Но кроме операции возведения в квадрат, существует еще операция возведения в куб, и у нее тоже есть своя обратная операция – извлечение кубического корня, которую еще называют корнем третьей степени. Символ кубического корня пишется также как и у квадратного только с маленькой тройкой:
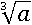
Чтобы извлечь кубический корень нужно подобрать такое число, куб которого равен подкоренному числу. Например, кубический корень из 8 равен двум, потому что два в кубе равно восьми:
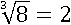
23=2∙2∙2=8
Наряду с операцией обратной возведению в куб есть и операция обратная возведению в четвертую степень – это извлечение корня четвертой степени, в его основе тот же принцип – он равен неотрицательному числу, четвертая степень которого равна подкоренному числу. Так корень четвертой степени из 81 равен 3, потому что 3 в четвертой степени равно 81:
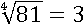
34=3∙3∙3∙3=9∙9=81
Но число 3 не единственное, четвертая степень которого равна 81, число −3 в четвертой степени тоже равно 81:
(−3)4=(−3)∙(−3)∙(−3)∙(−3)=9∙9=81
Поэтому, если выбор стоит между двумя такими вариантами, принято считать, что корнем из неотрицательного числа является только неотрицательное число. Это не единственный нюанс, который обязательно надо учитывать. Познакомимся поближе с сутью такого понятия как обратная операция.
Вот шесть примеров применения прямой операции – возведение в четную степень, которая из чисел 1, 2, 3 и −1, −2, −3 позволяет получить числа 1, 16 и 729:
12 = 1 (−1)2 = 1
24 = 16 (−2)4 = 16
36 = 729 (−3)6 = 729
Заметим, что какое бы число мы не возводили в четную степень, всегда получаются неотрицательные.
Изобразим все шесть прямых операций в виде следующей диаграммы. Каждая красная стрелка символизирует прямую операцию – возведение в четную степень: красная стрелка идет от 24 к 16, значит, 24=16. При этом ни одна стрелка не показывает на отрицательные числа −1, −16 и −729.

Применение обратной операции к числам 1, 16 и 729 должно назад возвращать числа 1, 2, 3 и −1, −2, −3, если это возможно. Тогда построим диаграмму, только с обратными операциями – извлечение корня четной степени, которые изображены синими стрелками, указывающими противоположное направление.
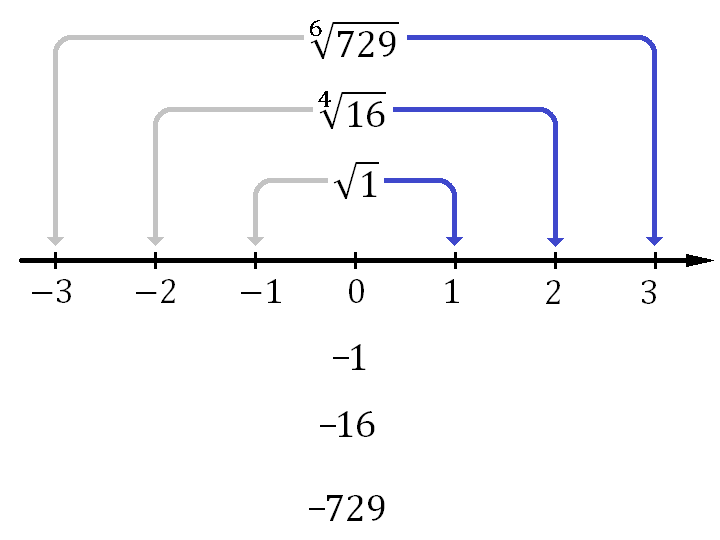
Кажется что, чтобы совершить обратную операцию нужно только перейти по синей стрелке, например, от 16. Вот только из 16 идут сразу две стрелки. Какую следует выбрать? Какое число 2 или −2 возвели в четвертую степень, чтобы получить 16? Выяснить это невозможно – оба числа в четвертой степени равны 16. Эта неопределенность и порождает все трудности.
Поэтому для однозначности принято считать, что корнем четной степени из положительного числа является только неотрицательное число. Стрелки, ведущие от чисел под корнем к отрицательному числу, изображены серым цветом – такие операции считаются недопустимыми в действительных числах и делать их нельзя. Значит, обратных операций будет уже только три:
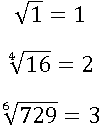
К тому же, как видите, ни одна из синих стрелок не идет от отрицательных чисел −1, −16 и −729, потому что ни одна красная стрелка не вела к этим отрицательным числам, невозможно вернуться оттуда, куда невозможно прийти. Поэтому в действительных числах и нельзя извлечь корень четной степени из отрицательного числа.
Теперь проведем такой же опыт, только уже с нечетными степенями. Вот шесть прямых операций с нечетными степенями:
23 = 8 (−2)3 = −8
35 = 243 (−3)5 = −243
47 = 16384 (−4)7 = −16384
Нарисуем на диаграмме красными стрелками каждую из этих прямых операций.
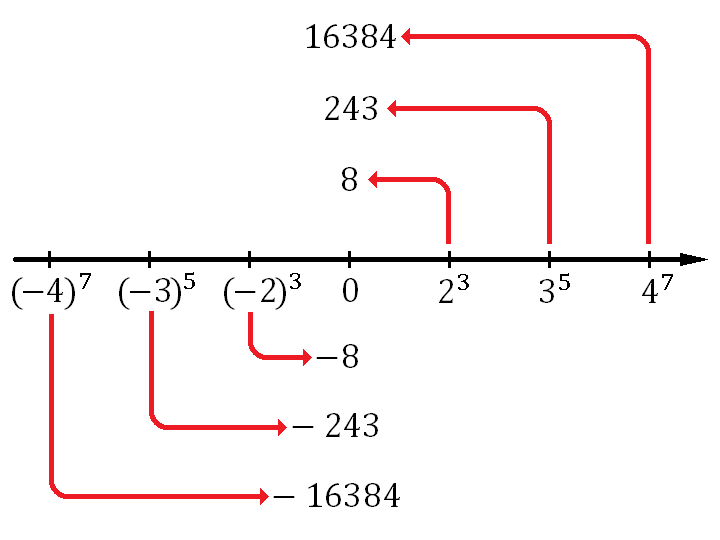
В отличие от предыдущей диаграммы с красными стрелками, здесь нет чисел, на которые показывают сразу две красные стрелки, благодаря этому не будет возникать неопределенности и обратные операции будут осуществимы для всех шести чисел.
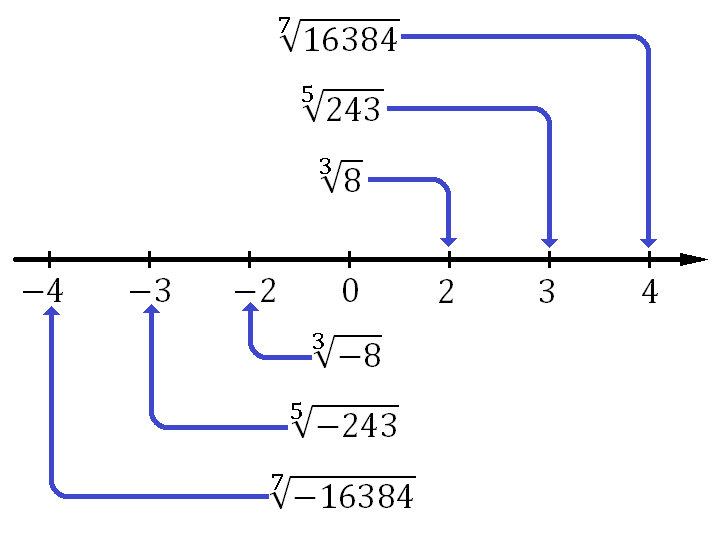
Значит, можно извлечь корни из всех чисел и получить точно такие же числа, которые возводили в нечетную степень:
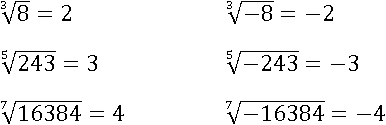
Совместим две диаграммы с синими стрелками, и тогда получим следующую картину.
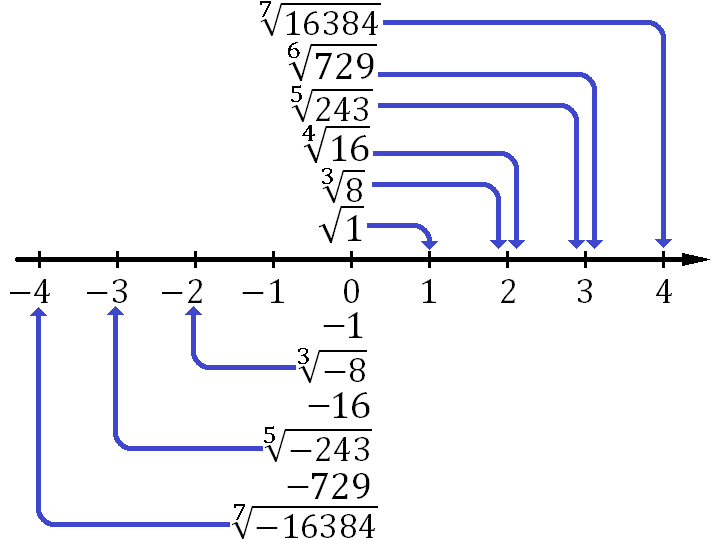
Можно сделать вывод: из неотрицательного числа можно извлекать корень любой степени, а из отрицательного можно извлекать корень только нечетной степени.
Дадим же определения корню любой натуральной (кроме первой) степени из неотрицательного числа и корню нечетной степени из отрицательного числа.
Корнем n-й степени из неотрицательного числа a называется такое неотрицательное число, при возведении которого в степень n получится число a:
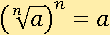
Корнем нечетной степени n из отрицательного числа a называется такое отрицательное число, при возведении которого в степень n получится a:
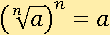
Например, корень пятой степени из 32 равен двум:
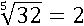
Потому что 2 в пятой степени равно 32:
25=2∙2∙2∙2∙2=32
Попробуем извлечь кубический корень из −27:
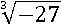
Известно ли нам число, куб которого равен −27? Известно, это −3:
(−3)3 = (−3)∙(−3)∙(−3) = 9∙(−3) = −27
Значит, кубический корень из −27 равен −3:
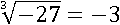
Корень пятой степени из 3125 равен 5:
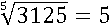
А корень седьмой степени из −128 равен −2:
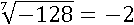
Из нецелого числа тоже может извлекается корень:
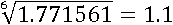
1.16=1.771561
Как и в случае с квадратным корнем, корень n-й степени может быть иррациональным числом, тогда возможно получить только его приближенное значение:
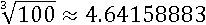
В таких случаях не пытаются извлекать корень или искать его приближенное значение, а оставляют его без изменений, т. к. это иррациональное число и больше ничего сделать не получится:
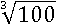
Очевидным должно быть, что и корень любой степени из нуля и единицы будут равны нулю и единице: