Переменные
У некоторых при виде буквы «икс» наступает ступор, им кажется, что это что-то невероятно сложное. На самом деле все гораздо проще: буква икс просто обозначает число, только не конкретное число, а вообще просто какое-то число.
Не всегда бывает заведомо известно, с какими числами придется иметь дело. Переменная почти всегда избавляет от необходимости знать эти числа заранее и позволяет производить с ними всевозможные действия, не беспокоясь об их значении. Например, к неизвестному числу x можно прибавить единицу, тогда получится такое число:
x+1
Или число x можно умножить на 2:
2∙x
Также можно x сначала умножить на 2 и к тому, что получится прибавить 1:
2∙x+1
Или наоборот: прибавить один к x и получившееся число умножить на 2:
(x+1)∙2
С выражениями, содержащими переменные, необходимо уметь производить действия, которые изменяют внешний вид выражения, не меняя его значения (например, чтобы упростить его). Рассмотрим некоторые простые примеры таких действий.
Пример № 1
Упростим следующее выражение, т.е. заменим его на более простое, но равносильное:
x+x+x
Тут должно быть все просто: сложение трех одинаковых чисел равносильно умножению этого же числа на 3:
x+x+x=3∙x
Получившееся равенство будет верно при абсолютно любом допустимом значении числа x, такие равенства называются тождествами. Искусство заменять равное равным в математике очень важно.
В равенстве легко убедиться, если заменить x на любое число, допустим на 5:
5+5+5=3∙5
По обе стороны от знака равно одно и то же число 15.
Пример № 2
Попробуем сложить следующие числа.
2∙x+3∙x
Каким выражением можно заменить число, которое получилось в результате сложения 2∙x и 3∙x? Первое слагаемое – это удвоенный x, а второе – утроенный x, значит, всего получится пять x. Следовательно, данное выражение можно заменить на 5∙x:
2∙x+3∙x=5∙x
Для проверки подставим вместо x в этот раз число 11, и получим верное равенство 55=55:
2∙11+3∙11=5∙11
22+33=55
Пример № 3
Вспомним теперь предыдущий урок и раскроем эти скобки (то есть заменим данное выражение на равносильное без скобок). Поступать с числом x при этом нужно совершенно также как и с любым другим числом при раскрытии скобок – умножить его на два, как и единицу:
2∙(x+1)=2∙x+2∙1
Выясним, будит ли первое выражение равно второму, если x=3:
(3+1)∙2=4∙2=8
И второе имеет значение 8:
2∙3+2∙1=6+2=8
Попробуйте подставить в оба выражения любое другое число, и вы опять получите одинаковое значение в обоих случаях.
Пример № 4
Раскроем скобки:
3∙(4∙x+7)
По всем правилам раскрытия скобок надо 3 умножить на 4∙x и 3 умножить 7, для этого нужно четко понимать, что 4∙x – это какое-то число, увеличенное в 4 раза, которое требуется увеличить еще в 3 раза. А какое число в 3 раза больше чем учетверенный x? Разумеется, 12∙x:
3∙(4∙x+7)=3∙4∙x+3∙7=
=12∙x+21
Пример № 5
Как умножать, делить и складывать дроби без переменных написано здесь. Дроби с переменными умножаются, естественно, по тем же правилам, что и без переменных – числитель на числитель, знаменатель на знаменатель:
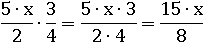
Пример № 6
При делении на дробь с переменной вторая дробь тоже переворачивается:
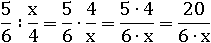
И сократим, разделив на 2 числитель и знаменатель, как того требует основное свойство дроби:
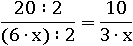
Получилось выражение тождественное первоначальному, только уже немного проще:
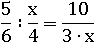
Пример № 7
Теперь сложим дроби с переменной. Сначала с помощью основного свойства дроби делаем знаменатели одинаковыми:
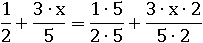
И складываем числители:
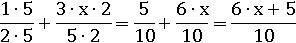
Получилось еще одно тождество:
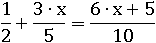
Подставьте вместо x число 10 – оба выражения будут иметь значение 6.5.
Пример № 8
Сложим дроби:
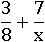
Переменная может встретиться и в знаменателе, в этом случае x все еще может быть каким угодно числом, но только не нулем (x≠0); потому что, если x=0, то число 7 во второй дроби поделится на ноль, чего делать нельзя:
Но и в этом случае потребуется общий знаменатель, поэтому первую дробь домножим на x, вторую - на 8:
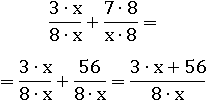
Пример № 9
Бывает и такое, что переменная есть везде:
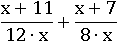
Конечно, можно первую дробь домножить на 8, а вторую – на 12, но можно найти числа и поменьше. При этом важно понимать, что домножать надо весь числитель и знаменатель:
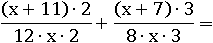
Оба знаменателя теперь равны 24∙x, значит, можно складывать:
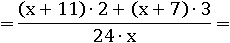
Раскроем скобки:
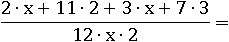
Заменим 11∙2 на равное ему 22, а 7∙3 – на 21 и переставим слагаемые для большего удобства:
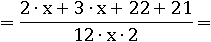
Заменим 2∙x+3∙x на 5∙x, 22+21 – на 43, а 12∙x∙2 – на 24∙x.
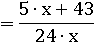
Подставим 1 в первое выражение:
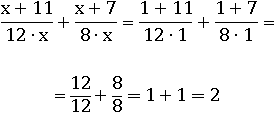
Подставим во второе:
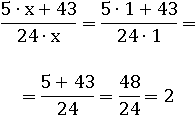
Очевидно, что полученным выражением проще пользоваться для вычислений, а результат оно будет давать точно такой же как первое.
Пример № 10
В предыдущих примерах мы заменяли каждый x в отдельном выражении на произвольное, но все же на одинаковое число, потому что одной и той же букве в одном выражении соответствует одно и то же число. Однако часто возникает необходимость подставлять именно разные числа, для этого просто используют другие латинские или греческие буквы, обозначающие другие переменные, которых можно будет заменять другими числами. Например, значение следующего выражения при x=2 и y=3 равно пяти:
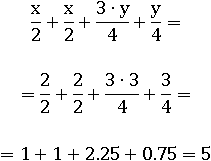
Заодно упростим это выражение. Сложим дроби, уже имеющие одинаковый знаменатель:
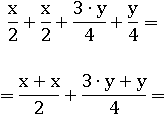
Заменим x+x на 2∙x и 3∙y+y на 4∙y:
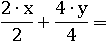
Сократим дроби, разделив числитель и знаменатель:
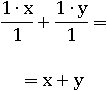
Выражение стало гораздо проще, и если x=2 и y=3, то очевидно, что получится тоже пять. Дальше упростить уже не получится – невозможно сказать чему будет равно одно неизвестное число плюс уже другое неизвестное число.
Пример № 11
Переменных может быть и гораздо больше. Отнимем одну дробь от другой:
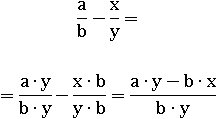
Пример № 12
Выражение не всегда становится проще, когда раскрывают скобку, иногда оно упрощается при вынесении общего множителя за скобку:
a∙x+a∙y−a∙z=a∙(x+y−z)
Гораздо проще сначала сложить все числа в скобках и потом один раз умножить, чем три раза умножать и три раза складывать.
Пример № 13
Иногда упрощение выражения бывает очень эффективным. Раскроем все скобки.
x∙(y−z)+y∙(z−x)+(x−y)∙z=
x∙y−x∙z+y∙z−x∙y+x∙z−y∙z=
От перестановки слагаемых сумма не меняется, поэтому переставим слагаемые для большей наглядности:
x∙y−x∙y+y∙z−y∙z+x∙z−x∙z
Что получится, если прибавить x∙y и отнять x∙y? От того, что к чему-то прибавляют какое-то число и потом его же отнимают, ничего не изменится. Значит, первые два члена можно просто заменить на ноль, ибо они ни на что не влияют, как и остальные две пары. Выходит, что первоначальное выражение при любых x, y и z будет равносильно просто одному числу ноль:
0+0+0=0
Проверим равенство. Пусть x=11, y=7, z=5:
x∙(y−z)+y∙(z−x)+(x−y)∙z=
11∙(7−5)+7∙(5−11)+(11−7)∙5=
11∙2+7∙(−6)+4∙5=
22−42+20=0
Действительно, выражение оказалось равно нулю. Что же значит, что в упрощенном выражении нет чисел x, y и z? Это значит, что значение первоначального выражения никак не зависело от x, y и z – вместо них могли быть какие угодно другие числа, и все равно получился бы ноль.