Тангенс на тригонометрической окружности
Здесь речь пойдет о тангенсе с котангенсом уже для любого угла от 0° до 360°. Постараюсь объяснить все также максимально просто, с большим количеством примеров и всевозможных иллюстраций, но будет гораздо проще, если сначала вспомнить самые азы тригонометрии из этой статьи.
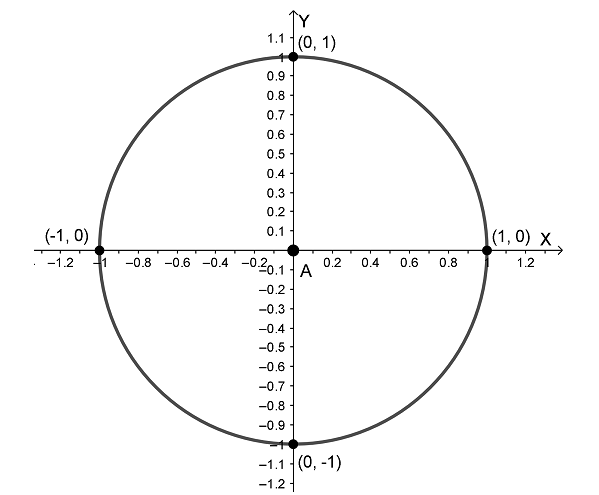
Возьмем всем известную систему координат, только нарисуем еще окружность с центром в начале координат (в точке A), радиус этой окружности обязательно должен быть равен единице. Таким образом у нас получилась так называемая тригонометрическая (или единичная) окружность. Пересекаться с осью X она будет в точке с координатами (1; 0) и точке (-1; 0), а с осью Y в точках (0; 1) и (0; -1).
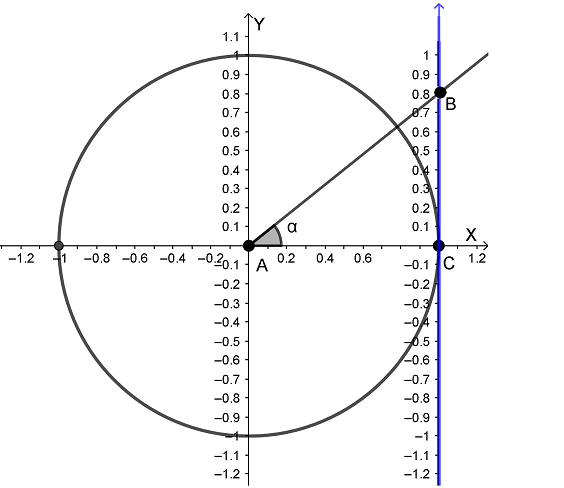
Теперь проведем еще одну ось через точку C параллельно оси Y и точно такую же как ось Y, называется она линией тангенсов. Затем проведем луч AB из точки A, пересекающий линию тангенсов в точке B. В результате получился прямоугольный треугольник ABC, где угол BAC мы для удобства обозначим греческой буквой α (читается «альфа»).
Как известно из вводной статьи, чтоб получить тангенс острого угла α надо длину стороны BC, противолежащей углу α, поделить на длину стороны AC, прилежащей к углу α:
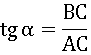
Для примера, определим тангенс 45-ти градусов. В треугольнике ABC отложим угол α равный 45°. Затем надо измерить длины сторон BC и AC. Но длину стороны BC измерять не надо – по линии тангенсов и так видно, что BC равно 1, т.к. координата точки B на линии тангенсов равна 1 (линия тангенсов сама является бесконечной линейкой); а сторона AC является радиусом, который в этой окружности всегда равен одному.
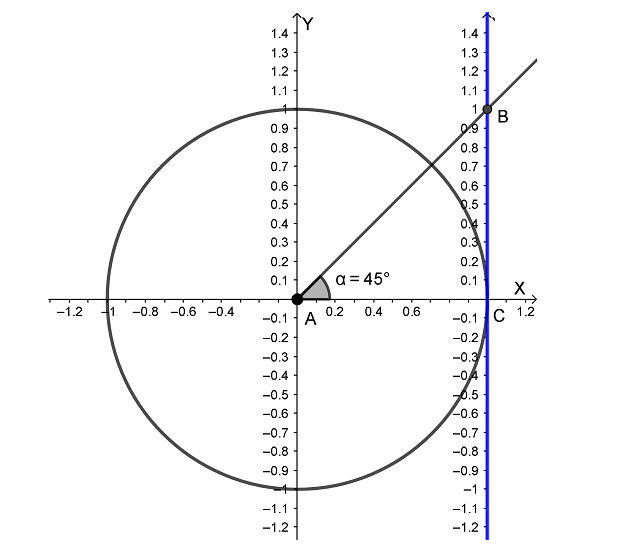
Значит, осталось лишь поделить длину BC на длину AC. Один разделить на один – будет один, следовательно, тангенс 45-ти градусов равен одному:
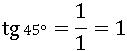
Очевидно, что независимо от угла α сторона BC всегда будет равна положительной координате точки B на линии тангенсов, а сторона AC при любом угле α равна 1. Получается, что нам нужно было просто координату точки B разделить на 1, но любое число при делении на 1 не изменяется. Значит, чтоб определить тангенс 45-ти градусов, достаточно было просто посмотреть на координату точки B на линии тангенсов – она и будет равна тангенсу 45-ти градусов.
Попробуем таким способом приближенно определить tg 30°. Нарисуем систему координат с единичной окружностью, отмерим угол α=30° и проведем луч AB.
Число 0,58 – это координата точки B на линии тангенсов, равная тангенсу 30°, значит, tg 30° ≈ 0,58.
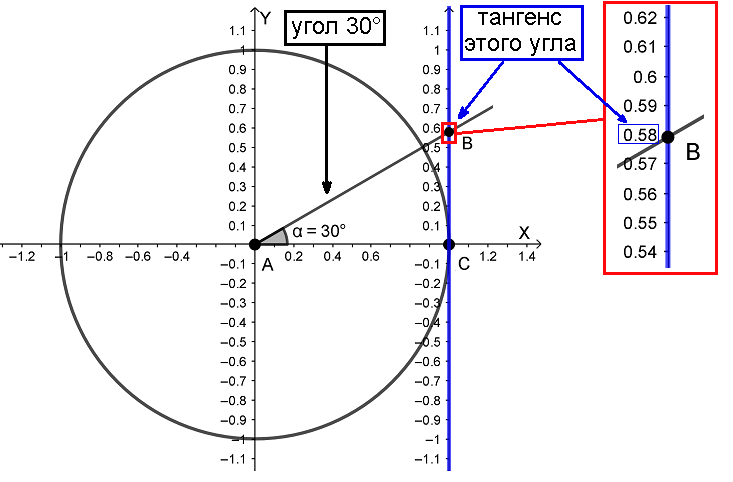
Теперь откроем калькулятор в компьютере и поставим его в инженерный режим. Проверим полученный результат.
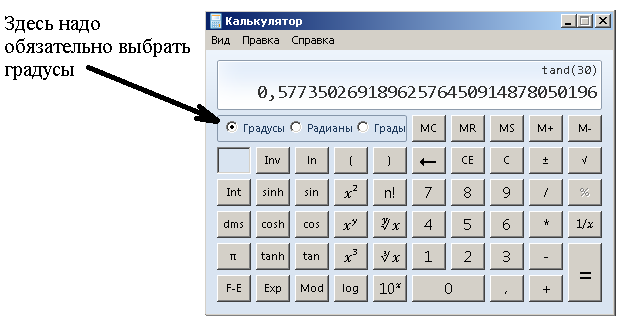
Калькулятор показал число очень похожее на 0,58 число, только точнее нашего. Но и результат калькулятора не идеален, абсолютно точное значение тангенса 30° равно числу 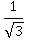 . Вычислить число
. Вычислить число 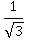 с помощью тригонометрической окружности не получится, его нужно будет запомнить. Но число 0,58 на линии тангенсов всегда будет очень хорошо напоминать, что на самом деле tg 30° =
с помощью тригонометрической окружности не получится, его нужно будет запомнить. Но число 0,58 на линии тангенсов всегда будет очень хорошо напоминать, что на самом деле tg 30° = 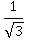 , потому что 0,58 ≈
, потому что 0,58 ≈ 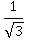 . В любом случае при решении школьных задач потребуется знать точные тангенсы только нескольких основных углов, и все они будут даны в конце этой статьи.
. В любом случае при решении школьных задач потребуется знать точные тангенсы только нескольких основных углов, и все они будут даны в конце этой статьи.
Но нам нужно научиться определять тангенс любого угла. А чему будет равен, например, тангенс угла 315°? Той же самой координате точки B на линии тангенсов, только в этот раз она будет уже отрицательной.
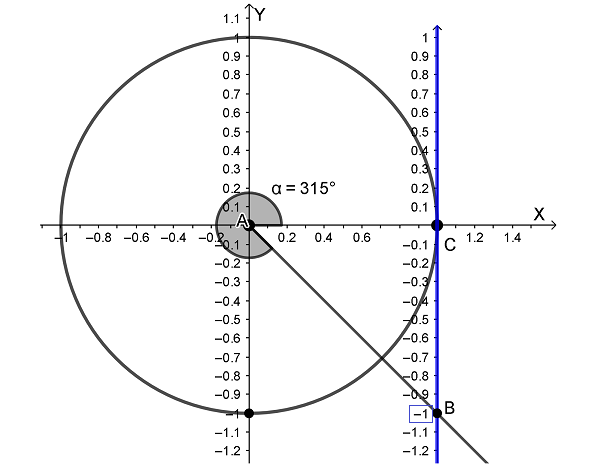
Теперь точка B на линии тангенсов указывает нам на число -1, а значит, tg 315° = -1. Посмотрим, что же выдаст калькулятор.
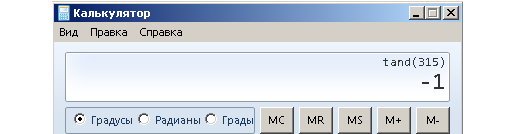
В этот раз нам и калькулятору удалось определить tg 315° абсолютно точно.
Но мы определили тангенс все еще не для всех углов. Проведем еще одну линию тангенсов параллельную оси Y через точку с координатами (-1; 0) , но уже направленную противоположно оси Y.
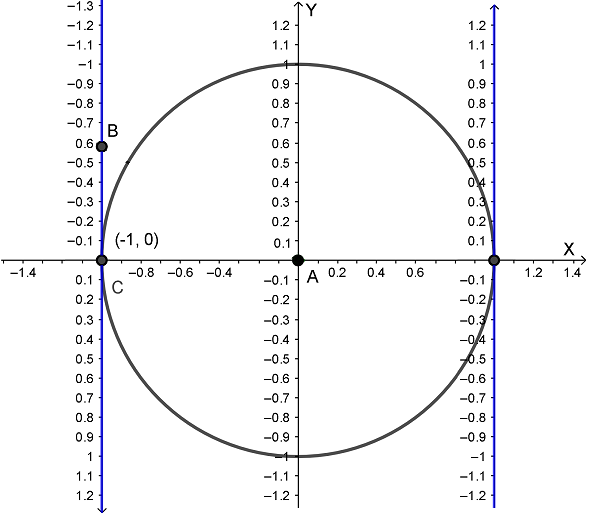
На этой новой оси тангенс угла α определяется абсолютно также: по координате точки B на второй линии тангенсов. Надо только помнить, что она направлена вниз, и положительная ее часть будет внизу, а отрицательная - вверху.
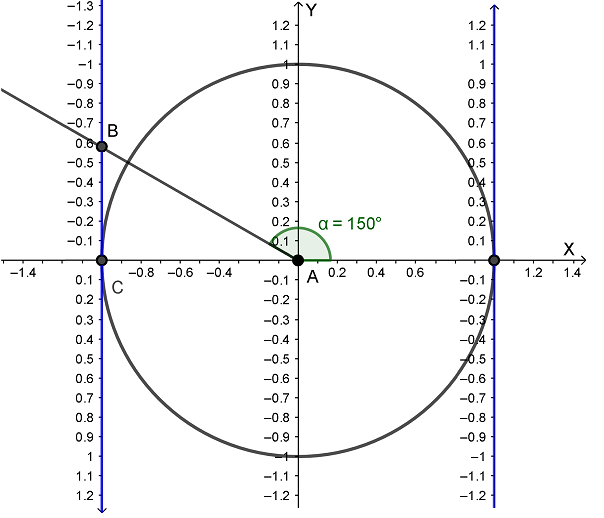
Попробуем приближенно определить tg 150°. Отмерим нужный угол 150°, проведем луч AB, и координата точки B на линии тангенсов покажет нам, чему равен tg 150°. Из рисунка видно, что tg 150° ≈ -0,58. Получилось то же число, какое было у tg 30°, только с минусом, значит точно: tg 150°= 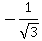 .
.
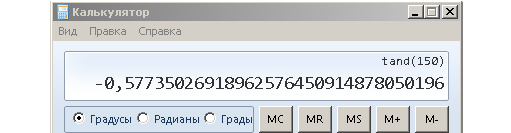
Калькулятор думает практически также.
Котангенс на тригонометрической окружности
Чтоб определить котангенс любого угла нам опять не обойтись без системы координат с тригонометрической окружностью. Проведем еще одну ось через точку (0; 1) параллельную оси X и абсолютно такую же как ось X, только называется она уже линией котангенсов. Затем проведем луч AB и из точки B опустим перпендикуляр BC из точки B на ось X.
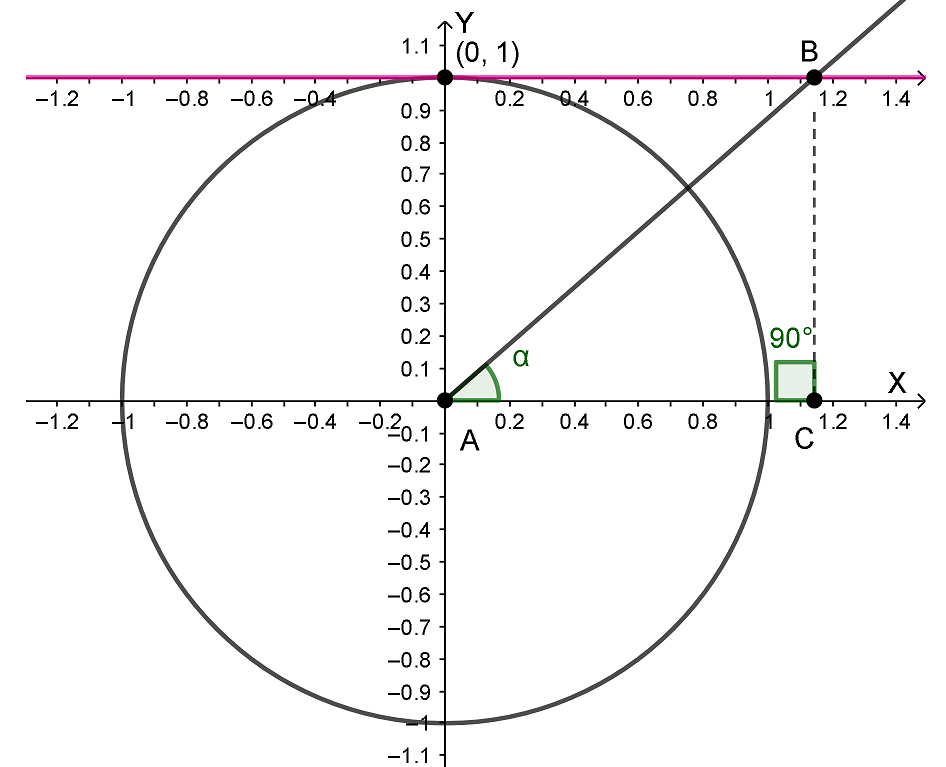
И у нас опять получился прямоугольный треугольник ABC, где угол BAC назовем α.
Из определения котангенса для острых углов известно: чтоб получить котангенс угла α нужно прилежащую к углу α длину стороны AC разделить на длину противолежащей к углу α стороны BC:
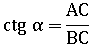
Очевидно, что при любом α длина стороны BC, как и радиус окружности, всегда равна единице, тогда:
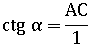
А при делении на единицу ничего не изменится, значит
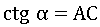
Т.е. котангенс угла α будет равен длине отрезка AC.
Не трудно заметить, что при любом α длина стороны AC полностью совпадает с положительной координатой точки B на линии котангенсов. А значит, ctg α будет всегда равен еще и координате точки B на линии котангенсов при всех α. Стороной AC будет не очень удобно пользоваться, поэтому вместо нее возьмем координату точки B на линии котангенсов. Именно эта координата точки B и будет являться котангенсом угла α.
Попробуем приближенно вычислить ctg 150°. Построим систему координат, начертим на ней единичную окружность, проведем линию котангенсов, отмерим угол 150°, проведем луч соответствующий этому углу.
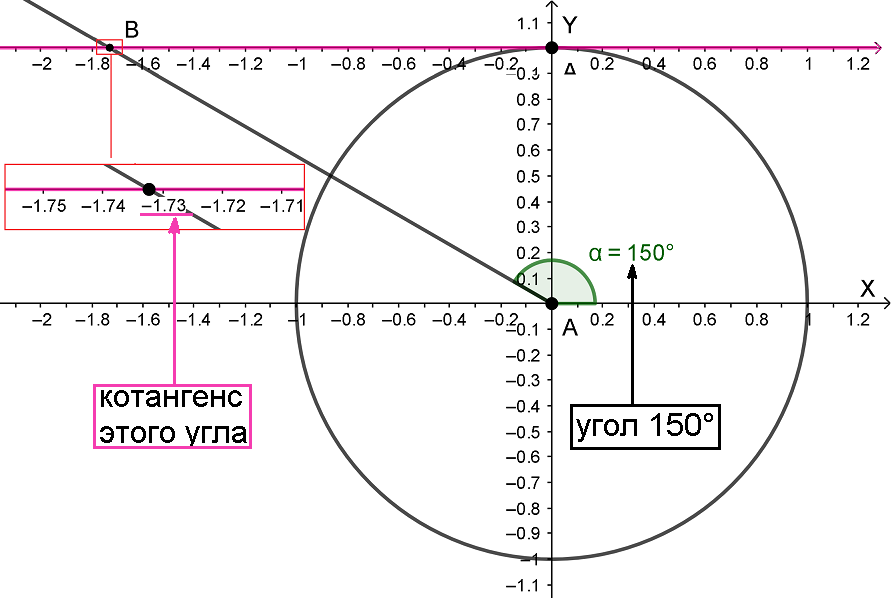
Луч AB пересек линию котангенсов на отметке -1,73, значит ctg 150° ≈ -1,73 (точно: ctg 150° = 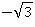 ).
).
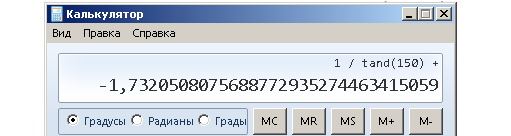
На калькуляторе нет котангенса. Чтобы вычислить ctg 150°, надо 1 разделить на tg 150°.
Осталось только определить котангенс для углов от 180° до 360°. Но этой линии котангенсов уже не хватает, поэтому начертим вторую линию котангенсов, проходящую через точку (0; -1), параллельную оси X, но направленную в противоположную сторону.
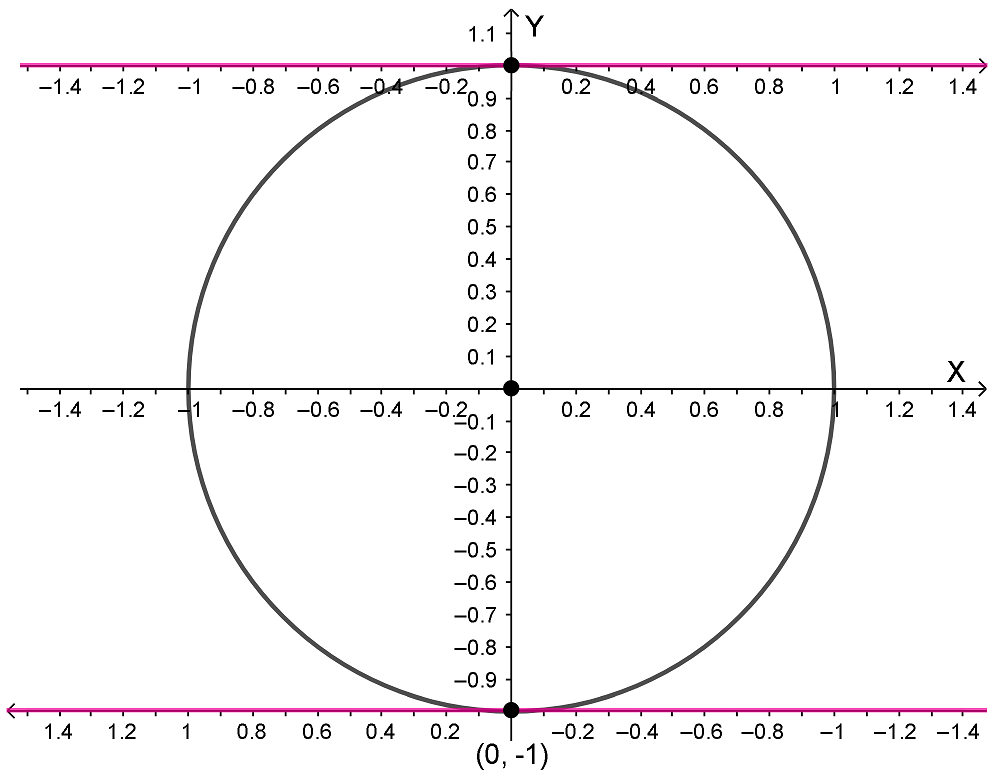
Координата пересечения второй линии котангенсов с лучом AB тоже будет равна котангенсу угла.
Рассмотрим на это на примере. Пусть требуется приближенно вычислить ctg 300°. На системе координат с единичной окружностью проведем луч AB так, чтобы угол α был равен 300°. Тогда луч AB пересечет вторую линию котангенсов где-то на числе -0,58. Значит, ctg 300° ≈ -0,58. Число -0,58 нам уже встречалось – это же 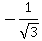 , а значит ctg 300° =
, а значит ctg 300° = 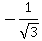 .
.
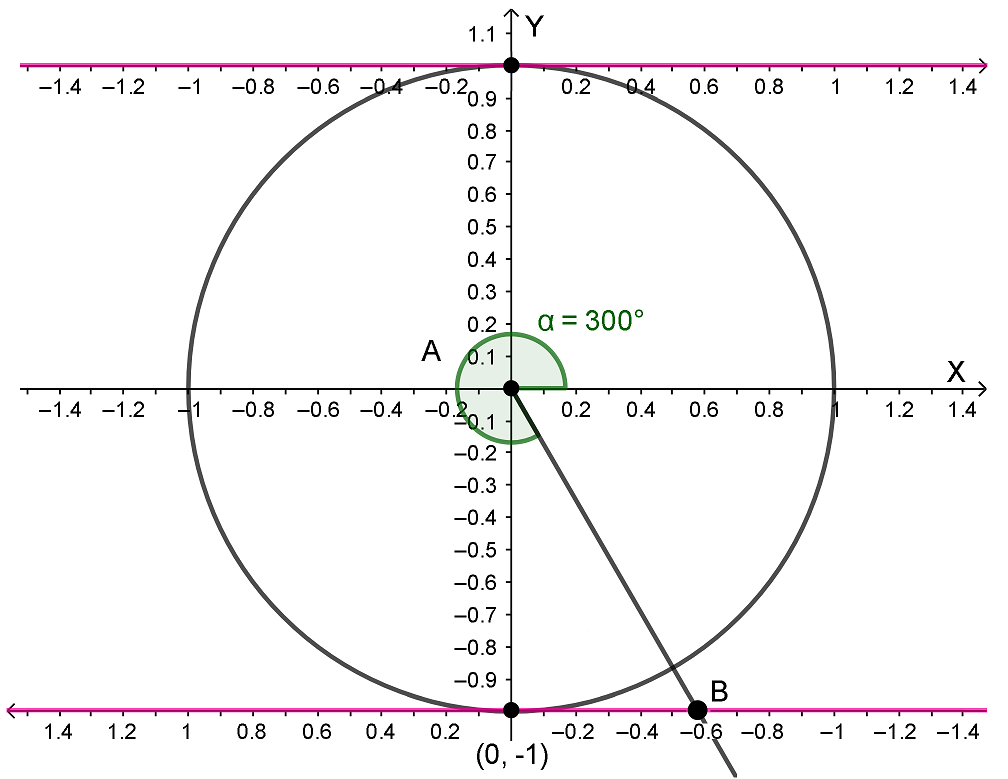
Если сравнить наш результат с калькулятором, то выяснится, что отклонение незначительное. Напоминаю: сначала вычисляем на калькуляторе tg 300°, запоминаем этот результат, затем один делим на число, которое запомнили - получаем ctg 300°.
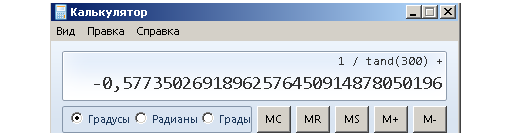
И калькулятор тоже так думает.
Теперь можно обобщить все полученные знания, изобразив на единичной окружности все линии тангенсов и котангенсов и уже точные значения всех нужных углов этих функций.
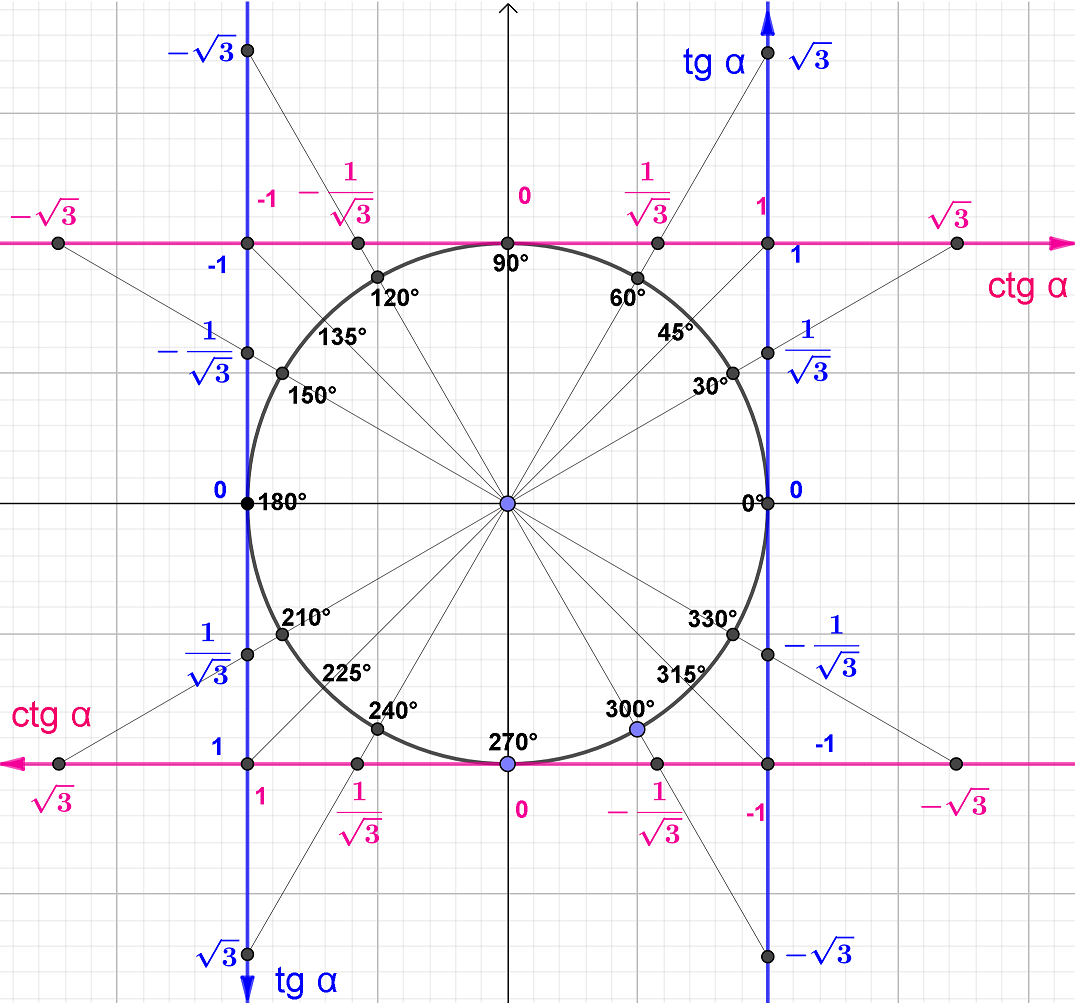
Чтобы определить тангенс или котангенс любого угла от 0° до 360°, достаточно на единичной окружности провести луч, соответствующий требуемому углу, и посмотреть в точке с какой координатой этот луч пересечет одну из линий тангенсов или котангенсов, эта координата и будет равна тангенсу или котангенсу требуемого угла.
Теперь, благодаря тригонометрической окружности, можно легко заметить многие свойства тангенса и котангенса, не прикладывая особых усилий. Например, если плавно увеличивать угол α от 0° до 90°, то tg α будет также возрастать, и чем больше угол α приближается к 90°, тем быстрее увеличивается его тангенс. Аналогично будет увеличиваться и ctg α, если α уменьшать от 90° до 0° или уменьшать от 270° до 180°. Уже можно увидеть, что tg 0° = 0, tg 180° = 0, ctg 90° = 0 и ctg 270° = 0. Настоятельно рекомендую убедиться во всем этом самостоятельно.
Следует обратить особое внимание, что когда угол α равен 90° или 270°, луч AB будет параллелен линиям тангенсов и не пересечет ни одну из них, поэтому тангенсов этих углов не существует, их вообще невозможно определить, выражения tg 90° и tg 270° не имеют смысла, как и деление на ноль. Также, когда угол ал равен 0° или 180° луч AB не пересечет линии котангенсов, значит сtg 0° и tg 180° не существует.
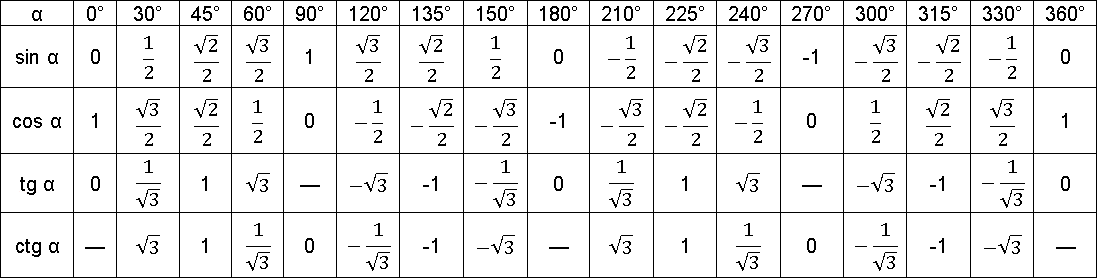
Определить все точные значения этих функций школьными методами нельзя, но это и не понадобится. Нужно знать только точные значения тангенса и котангенса углов, изображенных на предыдущем рисунке, но запомнить их в таком виде будет гораздо проще чем таблицу, изображенную ниже, да и без единичной окружности не получится решить многие другие задачи.