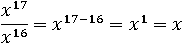Степень с натуральным показателем
Введем очередное новое понятие.
Чтобы сделать более удобной запись сложения одинаковых чисел, обычно используют умножение:
5+5+5+5=4∙5
Подобно этому для более компактной формы записи умножения большого количества одинаковых чисел существует операция возведения в степень
2∙2∙2∙2=24
Получившаяся запись называется степенью: число, 4 записанное в верхнем правом углу двойки, называется показателем степени, а сама двойка – основанием степени. Когда читают вслух подобную запись, говорят «два в четвертой степени»
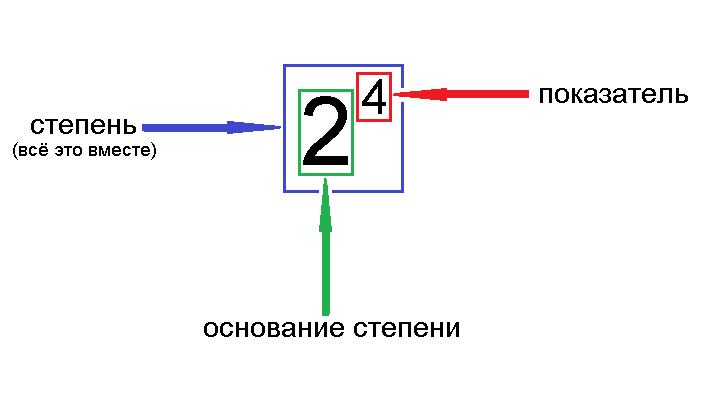
Показатель показывает, сколько раз основание (число a) умножается само на себя:
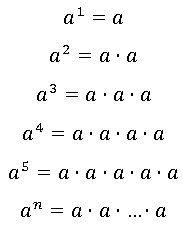
При этом степенью числа a , с показателем 1 называют само это число
a1=a
Например, два в четвертой степени будет равно 16:
24=2∙2∙2∙2=16
Три в пятой степени равно 243:
35=3∙3∙3∙3∙3=243
В степень можно возвести и нецелое число:
1.52=1.5∙1.5=2.25
А любое число в первой степени равно самому себе:
41=4
(−13)1=13
Если основанием степени является число a, и при этом показатель степени равен двум, то такое выражение можно называть не только «a во второй степени», но и «квадратом числа a» или просто «a квадрат»:
a2=a∙a
Например, квадрат двух равен четырем:
22=2∙2=4
А квадрат пяти будет равен двадцати пяти:
52=5∙5=25
Единица в любой степени будет равна единице, ноль в любой натуральной степени равен нулю:
17=1∙1∙1∙1∙1∙1∙1=1
06=0∙0∙0∙0∙0∙0=0
Когда показатель числа a равен трем, такую запись чаще называют «кубом числа a», чем «a в третьей степени»:
a3
Так, куб трех равен двадцати семи:
33=3∙3∙3=27
Отрицательное число, умноженное на отрицательное число, будет равно положительному числу (минус на минус дает плюс), поэтому любое отрицательное число в квадрате всегда равно положительному:
(−2)2=(−2)∙(−2)=4
А вот куб отрицательного числа будет отрицательным числом:
(−2)3=(−2)∙(−2)∙(−2)= 4∙(−2)=−8
И вообще, отрицательное число в четной степени равно положительному числу, а в нечетной – отрицательному:
(−2)2=4
(−2)3=−8
(−2)4=16
(−2)5=−32
(−2)6=64
(−2)7=−128
В качестве показателя мы брали только такие числа как 1, 2, 3,… и.т.д., т.е. такие числа, которые используют для счета или, например, для нумерации квартир (не бывает квартир с номером 2.5 или -8); такие числа называют натуральными. В следующих статьях мы обязательно расширим это понятие на все остальные числа, но перед этим необходимо познакомится со степенями с натуральным показателем.
Свойства степени
Но новое понятие позволяет нам использовать и новые возможности, иначе это понятие становится бесполезным и неинтересным
Свойства степени с натуральным показателем
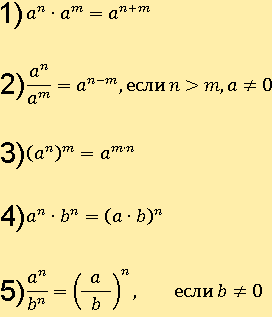
Теперь исследуем каждое из этих свойств на примерах.
Свойство № 1
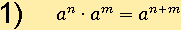
Данное свойство утверждает, что выражение в первой части равносильно выражению во второй части, чтобы проверить это утверждение, подставим вместо переменных числа. Пусть a = 2, n = 3, m = 4, тогда первая часть будет равна :
an∙am=23∙24=8∙16=128
Затем подставим эти числа во вторую часть свойства:
an+m=23+4=27=128
Действительно, свойство оказалось верным для данных чисел. Попробуем разобраться, почему так получается, что выражения вроде бы разные, а значения у них одинаковые.
Проанализируем что из себя представляет выражение в первой части. Заменим 23 на 2∙2∙2, а 24 на 2∙2∙2∙2:
23∙24=(2∙2∙2)∙(2∙2∙2∙2)
Получилось семь перемноженных друг на друга двоек:
(2∙2∙2)∙(2∙2∙2∙2)= 2∙2∙2∙2∙2∙2∙2
А двойка, умноженная семь раз на саму себя – это как раз 2 в седьмой степени:
2∙2∙2∙2∙2∙2∙2=27
Получается, что первое выражение состоит из трех двоек, умноженных друг на друга, которых домножили еще на четыре двойки – всего семь; а вторая часть состоит из семи перемноженных двоек. Значит, обе части – это двойка умноженная на саму себя семь раз.
Выходит, что никакой разницы между двумя способами вычисления нет и, значит, всегда можно 23∙24 заменить на 27 и наоборот.
На языке переменных это будет выглядеть так:
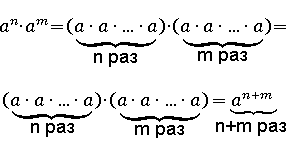
Это выражение верно для a, так как переменная a может быть любым числом, то получается, что данное свойство верно для любого числа, таким образом, вышеописанная запись через переменные является полноценным доказательством первого свойства.
Свойство № 2
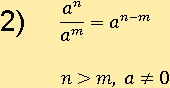
Подставим какие-нибудь числа в первую часть свойства:
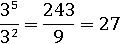
И подставим те же числа во вторую часть:
35−2=33=27
Обе части свойства представляют из себя одно и то же число, записанное в разном виде, поэтому оба выражения имеют одинаковое значение и свойство оказалось верным для этих чисел. Убедимся в этом, вычислив значение первой части другим способом:
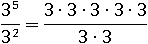
Далее остается лишь применить основное свойство дроби и сократить дробь, разделив числитель и знаменатель на 3 два раза:
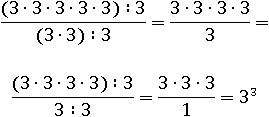
Выходит, что сокращая дробь, мы из пяти троек в числителе две убрали, осталось три тройки, которые равны 33, но то же самое мы делали, когда во второй части свойства отнимали 2 от 5.
Докажем это свойство:
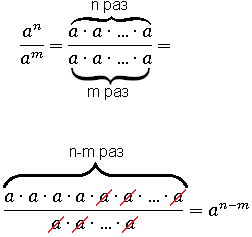
Таким образом, при умножении двух степеней с одинаковыми основаниями, степени складываются, (потому что множители добавляются) а при делении – отнимаются (потому что множители сокращаются). Эту закономерность нужно уметь видеть, а вот запоминать ее – бессмысленно.
Свойство № 3
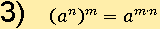
В первой части выражения заменим a на 2, n — на 3, m – на 2, и посмотрим, что получится:
(23)2=(8)2=8∙8=64
И произведем аналогичную замену во второй части:
23∙2=26=2∙2∙2∙2∙2∙2=64
Попытаемся выяснить в чем причина такого «совпадения».
Возьмем 23, которое равно 2∙2∙2:
23=2∙2∙2
При возведении 23 в квадрат 23 умножается на 23:
(23)2=23∙23
Значит, количество двоек увеличивается в два раза и становится равным шести:
(23)2=23∙23=2∙2∙2∙2∙2∙2
Но абсолютно то же самое происходит и когда в изначальном 23, умножается показатель на два – количество двоек увеличивается в два раза:
23∙2=2∙2∙2∙2∙2∙2
Получается, что возведение в квадрат 23 и умножение показателя в 23 на 2 производит одинаковый эффект – в этом заключается причина справедливости этого свойства.
Доказательство этого свойства будет таким:
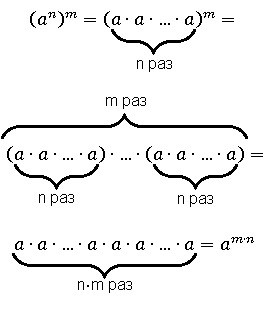
Свойство № 4
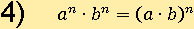
Посмотрим, что выйдет, если на месте переменных в первой части окажутся конкретные числа:
52∙32=25∙9=225
Во второй части все также:
(3∙5)2=152=15∙15=225
Все дело в том, что в первой части мы получили 225, умножив тройки и пятерки таким образом:
52∙32=5∙5∙3∙3
В то время как во второй части 225 получилось из тех же множителей, только расставленных в другом порядке:
(3∙5)2=(3∙5)∙(3∙5)=3∙5∙3∙5
А от перестановки множителей произведение не меняется:
5∙5∙3∙3=3∙5∙3∙5
Доказательство этого свойства:
Умножаем n штук a на n штук b.
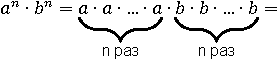
Переставляем — каждое b ставим рядом с a
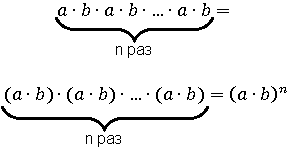
Свойство № 5
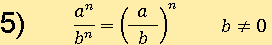
Это свойство мало чем отличается от предыдущего, поэтому сразу перейдем к его доказательству:
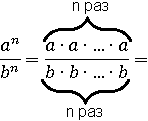
Правило умножения дробей позволяет сделать такое преобразование
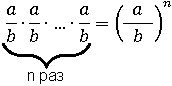
Рассмотрим несколько примеров упрощения выражений с помощью свойств степени.
Примеры
Пример № 1
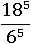
Разумеется, можно возвести 18 и 6 в пятую степень и разделить, но проще применить пятое свойство:
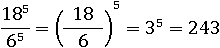
Пример № 2
24∙54
Многие любят упрощать такое выражение таким образом:
24∙54=16∙625=10000
Но гораздо удобнее применить четвертое свойство степени, ибо умножать в столбик трехзначные числа долго и трудоемко, а возводить 10 в степень легко и приятно:
24∙54=(2∙5)4=104=10000
Пример № 3
28
Не всегда нудных подсчетов в столбик удается избежать. Но и тут можно упростить вычисления — вместо того, чтобы восемь раз умножать на два, лучше два раза применим свойство № 3:
28=22∙4=(22)4=44=42∙2=(42)2=162=256
Также можно применить это свойство сразу дважды, а не по очереди:
28=22∙2∙2=((22)2)2=(42)2=162=256
И вместо семикратного умножения на 2 мы применили умножение лишь три раза: когда умножали 2∙2, 4∙4 и 16∙16.
Пример № 4
27∙0.56
Надеюсь, понятно, что это не самый удобный способ:
27∙0.56=128∙0.015625=2
Возводить 2 в седьмую степень – еще не так страшно, а вот 0.5 – в шестую уже страшновато, потом еще надо будет их умножать. Зато единицу возводить легко в любую степень, вот только там нет единицы, но ее можно получить – применим первое свойство:
27∙0.56=21+6∙0.56=21∙26∙0.56
Затем четвертое свойство:
21∙(2∙0.5)6
Вот и получилась единица 2∙0.5 равно одному:
21∙16=21∙1=21
Ну а что любое число в первой степени равно самому себе уже известно:
21=2
Пример № 5
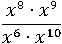
Воспользуемся сначала первым свойством:
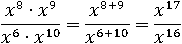
И чтобы выражение стало еще проще применим второе свойство: