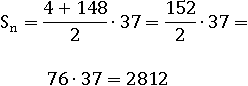Натуральные числа

• Обозначение натуральных чисел
• Однозначные, двузначные и трехзначные натуральные числа
• Многозначные натуральные числа
• Классы натуральных чисел
• Значение разряда натурального числа
• Позиционные системы счисления
• Примеры

Это самые доступные для понимания числа, которые всем были известны еще до первого класса. Их часто используют для обозначения целого количества каких-либо объектов или предметов, например, количество людей в городе или стране. Еще натуральными числами нумеруют всевозможные объекты: квартиры, дома, страницы в книге. Вот, например, 5 первых натуральных чисел:

1; 2; 3; 4; 5 ...

Не бывает квартир с номером 1.5 или минус третьей страницы в книге, поэтому числа −3 и 0.5 не являются натуральными. Но существует седьмая квартира и седьмая страница, поэтому 7 – натуральное число.

Количество натуральных чисел бесконечно и все они положительные. Один – наименьшее из них, число ноль уже не является натуральным. Самого большого натурального числа не существует – следующее число всегда будет больше, а предыдущее натуральное число – меньше: миллион больше тысячи, а миллиард больше миллиона и т. д:

1;   2;   3;   4;   5;   ... ;  100;   ... ;  1000;   ... ;  1000000;   ... ;  1000000000;   ... ;  9563615827;   ...

Множество натуральных чисел обозначается заглавной латинской буквой N. Когда хотят сказать, что число a является натуральным, пишут так:

a ∈ N

Такая запись означает, что число a принадлежит множеству N, в котором находятся только натуральные числа, а значит, и само a является натуральным.

Обозначение натуральных чисел

Все настолько привыкли к современному обозначению чисел, что уже мало кто задумывается о том, какой смысл несет в себе отдельная цифра в записи многозначного числа. Попытаемся понять этот смысл, это поможет при решении многих задачь.

Подобно тому, как для записи слов используют конечное количество букв из алфавита, для обозначения натуральных чисел используюстя десять специальных символов, которые называются цифрами:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Не следует считать, что цифра и число одно и то же, назвать цифрой число – это всё равно, что назвать буквой какое-нибудь слово; букв всего 33, а слов – сотни тысяч, цифр – только десять, а натуральных чисел – бесконечно.

Если воспринимать число как обозначение количества каких-либо предметов, например 735 яблок, то эта куча из 735 яблок состоит из 7 сотен яблок, к которым прибавили 3 десятка яблок и еще 4 яблока, получается, что:

735 = 7∙100 + 3∙10 + 1∙5

Таким образом цифра 7 показывает количество сотен, 3 – количество десятков, а 5 – количество единиц. Вышеуказанное выражение иногда удобнее записывать в таком виде, где маленькое число рядом с 10 обозначает количество нулей (степень 10 0=1; 10 1=10; 10 2=100; 10 3=1000 и т. д.):

735 = 7 ∙102 + 3∙101 + 5∙100

При этом последняя цифра всегда показывает количество единиц, предпоследняя – количество десятков и далее по мере продвижения справа налево на один знак значение того, количество чего показывает цифра, увеличивается в десять раз:

1000⟵100⟵10⟵1

10∙100⟵10∙10⟵1∙10⟵1

10∙102⟵10∙101⟵10∙100⟵100

В числе 8206 цифра ноль указывает на то, что количество десятков равно нулю, то есть их просто нет, и от сотен можно переходить сразу к единицам:

8206 = 8∙1000 + 2∙100 + 0∙10 + 6 = 8∙1000 + 2∙100 + 5∙1 = 7 ∙102+3∙101+5∙100

Однозначные, двузначные и трехзначные натуральные числа

Натуральные числа могут быть однозначными, двузначными и трехзначными.

В случае, когда число однозначное, оно состоит только из одной цифры, обозначающей количество единиц. Таких натуральных чисел всего 9:

1, 2, 3, 4, 5, 6, 7, 8, 9

Ноль – тоже однозначное, но ноль не является натуральным числом, поскольку принято считать, что натуральные числа начинаются с единицы.

Двузначные натуральные числа состоят из двух цифр, левая цифра показывает количество десятков, правая – количество единиц:

24 = 2∙10 + 4∙1

Всего натуральных двузначных чисел 90 штук от 10 до 99, например:

10; 14; 15; 23; 24; 30; 54; 99

Натуральные числа, состоящие из трех цифр, называются трехзначными, например, следующие числа трехзначные:

100; 112; 147; 293; 279; 320; 530; 999

Самое маленькое трехзначное 100, самое большое 999, всего их 900 штук. Кроме последних двух цифр, обозначающих количество десятков и единиц, в трехзначном числе есть еще первая цифра, указывающая на то, сколько сотен в числе, например, в числе 293 их две:

293=2∙100+9∙10+3∙1

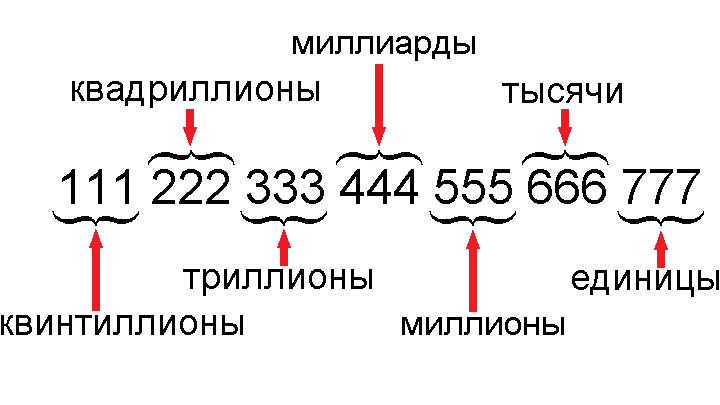
Многозначные натуральные числа

Все натуральные числа, которые состоят из более чем одной цифры, являются многозначными. Среди них встречаются двузначные, трехзначные, четырехзначные, пятизначные и т. д. Например, десятизначное число 1 234 506 789 является многозначным и содержит цифры обозначающие количество входящих в него тысяч, сотен тысяч, миллионов и многое другое. Далее указано, количество чего обозначает каждая цифра в этом натуральном числе:

• 9 – единицы
• 8 – десятки
• 7 – сотни
• 6 – тысячи
• 0 – десятки тысяч
• 5 – сотни тысяч
• 4 – миллионы
• 3 – десятки миллионов
• 2 – сотни миллионов
• 1 – миллиарды

Классы натуральных чисел

Часто для удобства большие мгогозначные числа разделяют пробелами на группы по три цифры, которые называют классами. Например, вот запись числа без разделения на классы:

1618033989

А вот то же число уже разбитое на четыре группы:

1  618  033  989

Во втором случае это число гораздо лучше воспринимается и его легче читать. Каждый класс (кроме самого левого) всегда состоит только из трех цифр, а самый левый в зависимости от длинны числа может содержать три, две или одну цифру как в этих числах:

137  695

93  646

7  345

625

36

9

Все классы называются по-разному: в числе 73 254 364 643 123 самый правый класс 123 называется классом единиц, следующий 643 – класс тысяч, затем 364 – класс миллионов, 254 – класс миллиардов, 73 – класс триллионов, существует и много других классов, такие как квадриллион, квинтиллион, секстиллион и другие, но они используются крайне редко.

Значение разряда натурального числа

Уже можно заметить, что значение натурального числа зависит не только от того, из каких цифр состоит число, но и от того, на каком месте (позиции) стоят эти цифры. Позиция, на которой стоит какая-либо цифра в натуральном числе, назыается разрядом. Например, в числе 321 цифра 1 стоит в разряде единиц и поэтому обозначает количество единиц, цифра 2 находится в разряде десятков, а 3 стоит в разряде сотен. У каждого разряда есть свое название: разряд единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов, десятков миллиардов, сотен милиардов, триллионов и т. д.

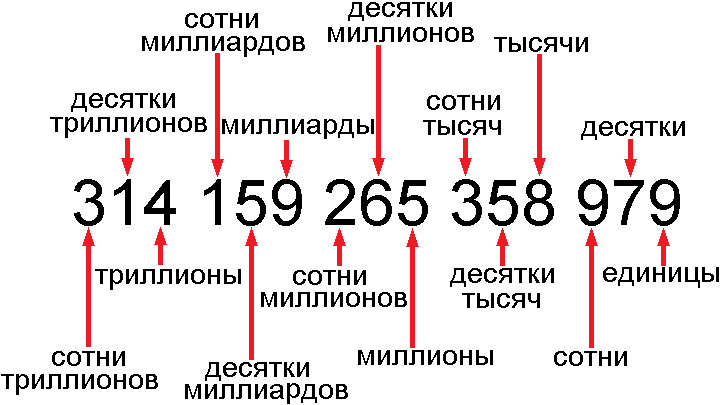
Разряды между собой не равноправны: существуют старшие и младшие разряды: чем левее стоит цифра, тем старше ее разряд. Так в числе 1 456 789 цифра 4, стоящая в разряде сотен тысяч, старше разряда цифры 5, которая находится правее в разряде десятков тысяч. Низший разряд единиц в этом числе занимает цифра 9, а высший разряд миллионов занимает единица.

Позиционные системы счисления

Данный метод записи натуральных чисел с помощью десяти цифр называется позиционной десятичной системой счисления, так как в ней используется десять цифр. А позиционной она называется, потому что значение числа зависит не только от того, из каких цифр оно состоит, но и от того какую позицию в этом числе занимает каждая цифра. Благодаря чему дополнительную информацию содержит позиция, которую занимает эта цифра, что и делает такую запись более компактной, удобной и наглядной.

Такой способ записи чисел далеко не единственный, бывают и другие системы счисления, в том числе и непозиционные. Например, существует двоичная позиционная система счисления, в ней числа состоят только из двух цифр 0 и 1, число 50 в двоичном виде выглядет так:

110010

Пример № 1

Перечислим все натуральные числа по порядку, начиная с самого наименьшего из них – единицы:

1; 2; 3; 4; 5

Следующее число 6 уже не удовлетворяет условиям задачи, потому что шесть не меньше шести. Поэтому в ответ пойдут только эти пять чисел.

Пример № 2

Сумма шести последовательных натуральных чисел равна 435. Найдите наименьшее из этих чисел.

Последовательными называются числа, которые идут друг за другом, например, после 10 идет 11, затем 12 и т. д.

Пусть x – это наименьшее из этих шести чисел, тогда следующим числом будет x+1, затем x+2. Получается, что все шесть чисел можно записать следующим образом:

x;  x+1;  x+2;  x+3;  x+4;  x+5

Cумма этих чисел равна 435, это значит, что если сложить все шесть чисел, то получится 435. Тогда можно составить следующее уравнение:

x + x + 1 + x + 2 + x + 3 + x + 4 + x + 5 = 435

От перестановки слагаемых сумма не меняется, поэтому расположим слагаемые в другом порядке для более удобного восприятия:

x+x+x+x+x+ x+1+2+3+4+5 = 435

Сложим все x и числа в левой части уравнения:

6x+15 = 435

Перенесем 15 в другую сторону и отнимем:

6x = 435−15

6x = 420

И разделим обе части на 6:

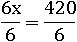
x=70

Это и есть то самое искомое наименьшее число из шести последовательных, что можно легко проверить:

70+71+72+73+74+75=435

Пример № 3

Чтобы понять как решить эту задачу, сначала напишем все натуральные числа, при сложении цифр которых получится 3:

111;  21;  12;  3

Если сложить все цифры в числе 111, то получится 3:

1+1+1 = 3

То же получится при сложении цифр в числах 21, 12 и 3:

2+1 = 3

1+2 = 3

3 = 3

Какое из этих четырех чисел наименьшее? Очевидно, что любое трехзначное число больше любого двузначного, а любое двузначное больше всякого однозначного. А из чисел 21 и 12 больше то, в котором первая цифра больше. Вывод: чтобы число было наименьшим, нужно подобрать его так, чтобы количество цифр (разрядов) в нем было минимальным, и первые цифры были поменьше.

Таким образом, чтобы снизить количество цифр, но при этом оставить сумму цифр равной 101, нужно написать много девяток:

99 999 999 999

Но если сложить все цифры в образовавшемся числе, то получится только 99, тогда придется увеличить количество разрядов, добавив двойку в начало числа, чтобы первая цифра была наименьшей:

299 999 999 999

Если сложить все цифры в этом числе, то получится 101:

2+9+9+9+9+9+ 9+9+9+9+9+9 = 2+9∙11 = 2+99 = 101

Пример № 4

Выпишим первые несколько чисел кратных четырем:

4; 8; 12; 16; 20; ...

А вот последние числа, которые делятся на 4, но не превышают 150:

...; 136; 140; 144; 148

Разделим самое большое из этих чисел на 4, и так узнаем, сколько всего существует чисел кратных четырем от 1 до 150:

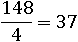
Значит, всего таких чисел 37 штук. Теперь все их нужно как-то сложить, в этом нам поможет одна из формул суммы первых членов арифметической прогрессии:

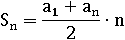
В нашем случае значения переменных в формуле такие:

a₁=4;     a_n=a₃₇=148;     n=37

Осталоть лишь посчитать сумму первых 37-ми членов нашей последовательности:

© Кирилл Морковкин & Машка Кулибякина