Свойства корня n-й (любой) степени

• Свойство № 1
• Свойство № 2
• Свойство № 3
• Свойство № 4
• Свойство № 5
• Примеры

Свойства – это некие характерные особенности, которое есть у какого-либо объекта или явления. Например, у снега есть свойства – он белый и холодный. И корень тоже имеет свои свойства.

В разделе примеры будет показано то, насколько свойства корня облегчают многие вычисления, а не являются каким-то дополнительным обременением.

Ни в коем случае не нужно пытаться вызубрить все эти свойства, достаточно просто иногда заглядывать в них в случае необходимости, и тогда все они со временем станут так же самоочевидны как и то, что снег холодный.

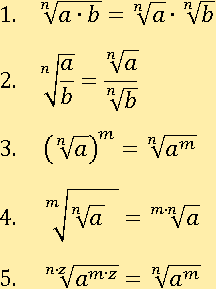
Проверим и докажем все свойства.

Свойство № 1

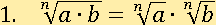
Чтобы лучше понять какую закономерность содержит в себе свойство, его надо применить к числам.

Пусть a=8, b=27, n=3, тогда первая часть свойства будет равна:

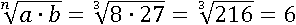
Вторая часть при этих же значениях переменных будет равна:

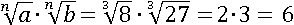
Теперь стало понятнее, какую закономерность несло в себе первое свойство.

Доказательство

По определению корня n-й степени, если возвести первую часть равенства в степень n, то получится подкоренное выражение:

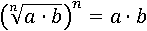
Первая часть свойства в степени n равна a∙b. Теперь возведем в степень n вторую часть, если получится тоже a∙b, значит, свойство будет доказано:

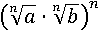
Заменим возведение в n-ю степень n-кратным умножением:

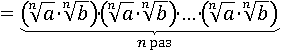
Переставим множители:

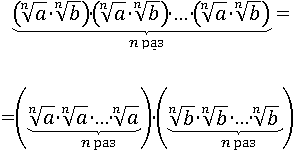
Что в свою очередь будет равносильно возведению в n-ю степень каждого множителя в обоих скобках:

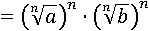
И по определению корень n-й степени из числа, возведенный в n-тую степень равен этому числу:

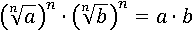
Так мы возвели обе части равенства в одинаковую степень n и получили a∙b в обеих частях, а такое возможно, только если обе части были равны. Свойство доказано.

Свойство № 2

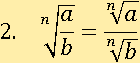
Пусть a=16, b=625, n=4, тогда первая часть будет равна:

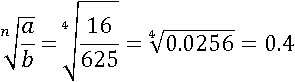
Посмотрим, чему будет равна вторая часть:

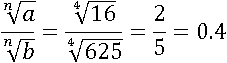
Доказательство

Поступим тем же образом и возведем первую часть этого свойства в степень n:

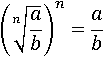
Возведем вторую часть, а потом посмотрим будет ли там тоже :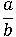

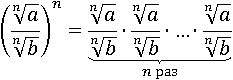
Получившиеся дроби умножим (как умножаются дроби см. здесь):

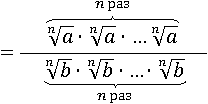
Умножение n раз – это возведение в n-ю степень:

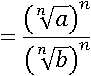
Вторая часть опять оказалась равна 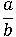после возведения в степень n, значит, обе части свойства были равны с самого начала:

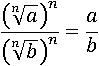
Свойство № 3

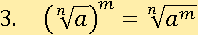
Пусть a=243, m=2 n=5

Вычислим значение первой части:

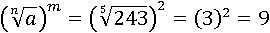
Вторая часть при этом будет равна:

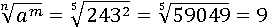
Доказательство

Избавимся от степени m, заменив ее m-кратным умножением:

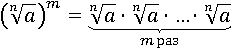
Используем уже доказанное первое свойство, заменив произведение корней на корень произведения:

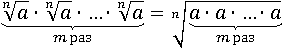
Под знаком корня m раз перемноженное a можно заменить на am:

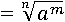
Что полностью совпадает со второй частью свойства.

Свойство № 4

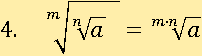
Пусть a=4096, n=4, m=3, тогда первая часть будет равна двум:

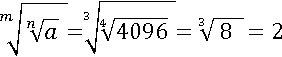
Вторая часть тоже равна двум:

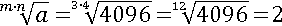
Доказательство

Возведем вторую часть равенства в степень n∙m, т.е. умножим вторую часть на себя столько же раз сколько получится, если умножить n на m:

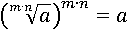
Теперь возведем первую часть в степень n∙m:

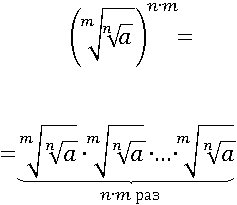
Разобьем все эти множители на n групп по m в каждой:

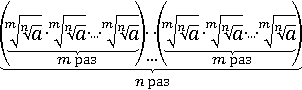
В каждой из n скобок умножается m раз сам на себя один и тот же множитель, заменим умножение m раз на себя возведением в m-ю степень:

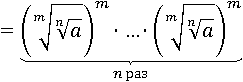
По определению корень m-й степени, возведенный в степень m будет равен подкоренному числу, значит можно заменить одно другим, т.к. определение говорит нам, что это одно и то же:

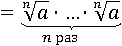
Получившееся умножение одинаковых множителей опять заменим на возведение в степень n:

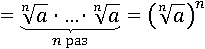
Еще раз применим определение корня, после чего выражение примет уже совсем простой вид:

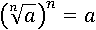
После возведения в степень n∙m обе части стали равны a, значит, они были равны и до возведения в эту степень.

Свойство № 5

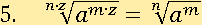
Пусть n=3, m=6, z=2, a=2.

При этих значениях переменных первая часть будет равна четырем:

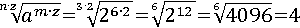
Вторая тоже равна четырем:

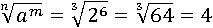
Доказательство

Воспользуемся только что доказанным четвертым свойством, и преобразуем первую часть равенства:

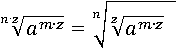
Применим третье свойство степени и заменим am∙z на (am)z:

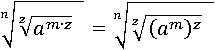
И по определения корня n-й степени заменим 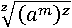на am:

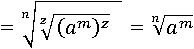
Так, поочередно выполняя равносильные замены равного равным, мы из первой части свойства получили вторую часть, доказав этим пятое свойство.

Примеры

Рассмотрим некоторые примеры упрощения выражений с помощью свойств корня n-й степени.

Пример № 1

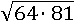
Можно сначала умножить, а потом долго подбирать число, квадрат которого равен 5184:

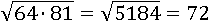
Но лучше применим первое свойство и извлечем корень из меньших чисел:

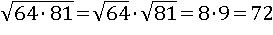
Так вычисления станут гораздо проще и, следовательно, точнее: во-первых – не требуется перемножать все числа под корнем; во-вторых – извлекать корень из двухзначных чисел на много легче чем из четырехзначных. Другими словами, мы используем корень для уменьшения чисел под корнем, и только потом умножаем уже маленькие числа, таким образом, на самом деле корень упрощает здесь вычисления, а не усложняет.

Пример № 2

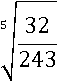
Разделить или хотя бы сократить эту подкоренную дробь и извлечь корень будет не просто, применим второе свойство:

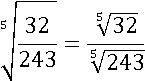
И корень из 32 и 243 извлечь уже можно:

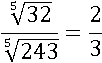
Пример № 3

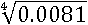
Довольно неудобное число для извлечения корня, а вот 81 – уже удобное. В таком случае заменим его на удобную дробь:

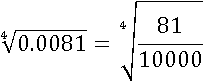
И применим второе свойство:

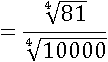
Теперь все корни удобные:

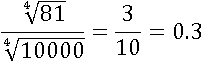
Пример № 4

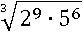
Делать так не рекомендуется:

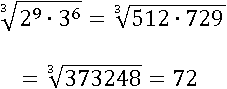
Лучше применим сначала первое свойство:

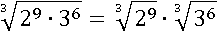
Затем слегка видоизменим:

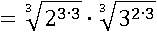
Применим третье свойство степени:

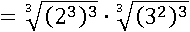
И с помощью определения корня n-й степени избавимся и от кубического корня, и от куба:

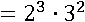
Вычислим окончательное значение:

23 ∙32=8∙9=72

Пример № 5

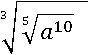
Воспользуемся четвертым свойством и заменим 10 на 2∙5:

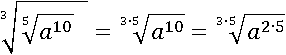
И даже не будем умножать 3 на 5, а лучше прибегнем к пятому свойству:

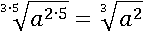
Еще больше упростить такое выражение уже не получится.

Пример № 6

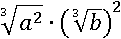
К первому корню применим третье свойство:

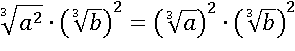
Вспомним четвертое свойство степени и вынесем квадрат за скобку:

И первое свойство корня:

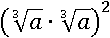
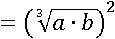
Дальше упростить не получится, но с конечным выражением будет легче работать.

Пример № 7

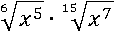
Хорошо было бы занести множители под один корень, но первое свойство корня позволяет делать такое только когда степени корня одинаковые. В таком случае воспользуемся пятым свойством корня и сделаем степени корня удобными:

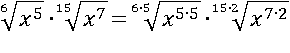
Теперь оба корня одной 30-й степени:

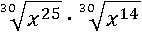
И первое свойство корня можно использовать:

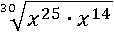
С помощью первого свойства степени упростим подкоренное выражение:

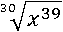
Числа 30 и 39 можно заменить следующим произведением:

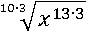
Затем снова прибегнем к пятому свойству степени и избавимся от тройки:

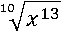
Подкоренное выражение можно представить в таком виде:

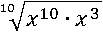
Разнесем множители по отдельным корням:

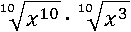
А корень 10-й степени из x10 – это x:

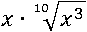
В следующей статье мы изучим новый математический инструмент, и с его помощью сделаем этот же пример более простым способом.

© Кирилл Морковкин & Машка Кулибякина