Синус

Каждый знает знает, что есть в школьной математике такое слово как синус, косинус, тангенс и котангенс, но все ли действительно понимают что это такое? В этой статье будет правильно и главное максимально просто рассказано об этом. Если посмотреть в школьный учебник по геометрии за 7-9 класс, то там будет написано следующее:

Чтобы понять что это значит, надо взять треугольник, в котором один угол будет 90°, т.е. прямоугольный треугольник. Сторона ВС называется катетом противолежащим углу А, сторона АС называется катетом прилежащим к углу А. Сторона АВ лежащая против угла 90° - это гипотенуза, она является всегда самой длиной стороной прямоугольного треугольника.

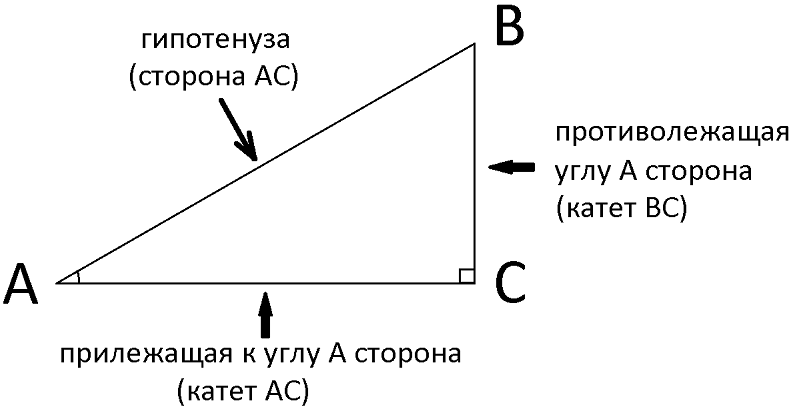
Тогда для того, чтобы вычислить синус угла А, надо найти противолежащую этому углу А сторону - в нашем рисунке это будет сторона ВС, измерить эту сторону, затем измерить самую длинную сторону АВ (гипотенузу) и разделить длину ВС на длину АВ. И тогда получившееся число будет синусом угла А.

Например, нам надо приближенно вычислить синус 30°, начертим прямоугольный треугольник и измерим противолежащую углу в 30° сторону ВС и сторону АВ. После измерения выяснилось, что катет BC=5 см, а гипотенуза AB=10 см. Делим 5 на 10 и получаем 0.5 - это и будет синус 30°. Стороны могли бы быть какой угодно длины, например, 7 см и 14 см, или 6,8 см и 3,4 см, но, если угол А равен 30°, а угол С будет 90°, то синус все равно будет около 0,5.

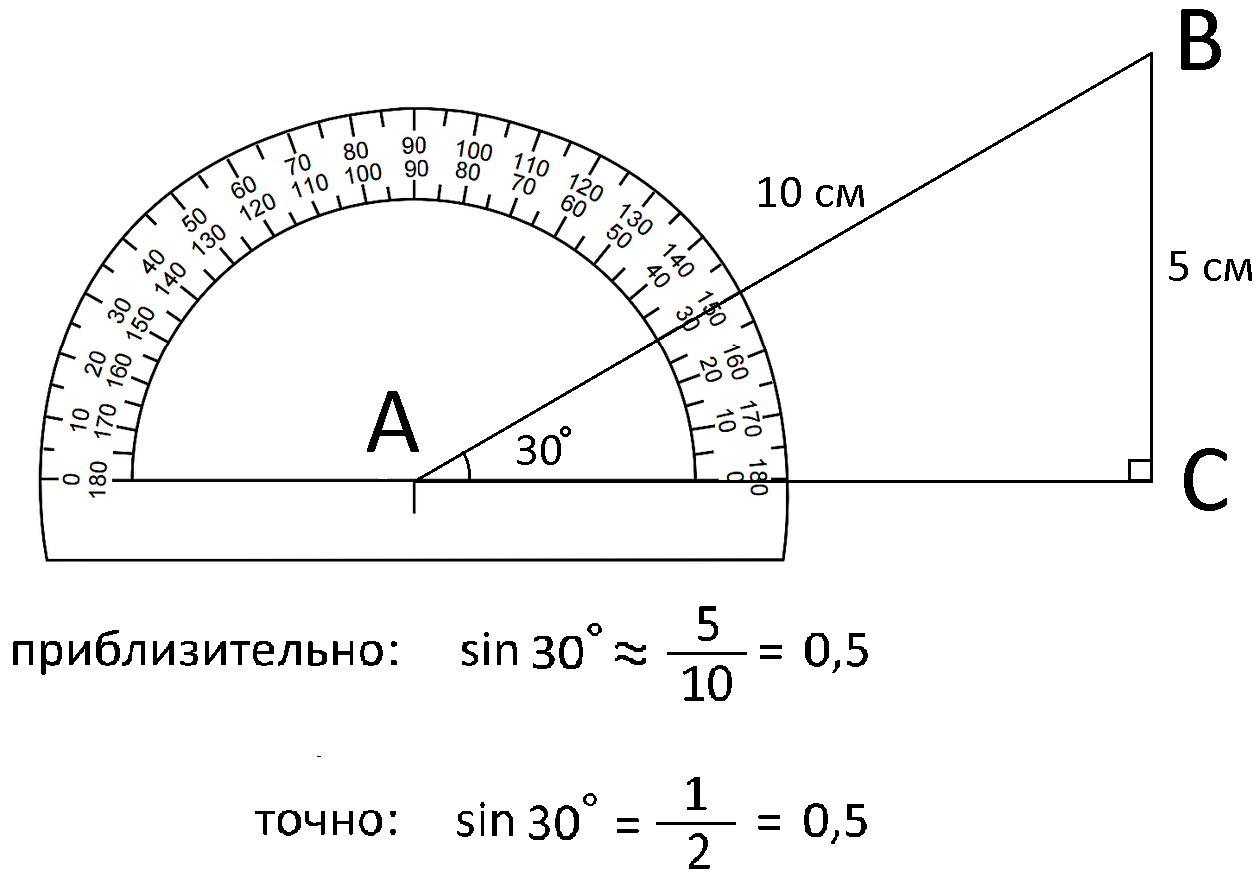
Точное значение синуса, косинуса, тангенса и котангенса таким способом определить не удастся, потому что невозможно начертить идеальный треугольник и абсолютно правильно его измерить, но это и не понадобится, для школьных задач просто нужно будет помнить только значения основных углов этих функций - 30°, 45° и 60°. Таблица с точными значениями синуса и косинуса этих углов будет дана ниже.

Вычисленные синусы любых углов меньших 90° (и не только синусы) можно легко проверить с помощью калькулятора. Для этого достаточно начертить произвольный прямоугольный треугольник, измерить в нем угол, противолежащий ему катет и гипотенузу, разделить длину измеренного катета на длину измеренной гипотенузы и записать получившееся число.

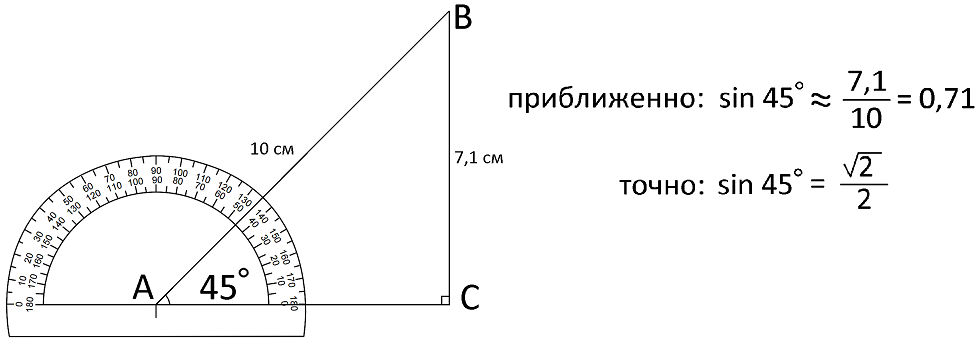
Проверим полученное приближенное значение синуса: возьмем инженерный калькулятор или его инженерную версию в компьютере (только надо поставить единицу измерения - градус, а не радиан), и попробовать вычислить на калькуляторе синус того же угла, что и был в треугольнике; то получиться должно примерно то же число.

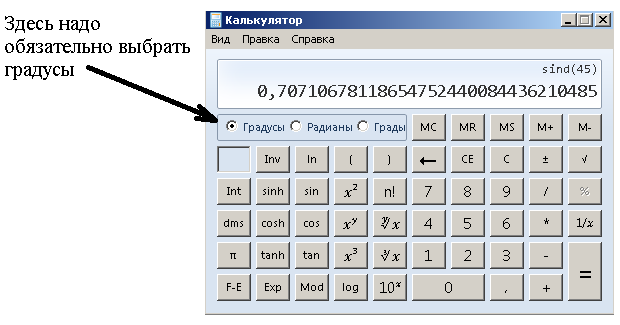
Вычисленный нами синус 45° очень похож на то, что нам показывает калькулятор, значит мы все правильно посчитали.

То же попробуем с углом 60°.

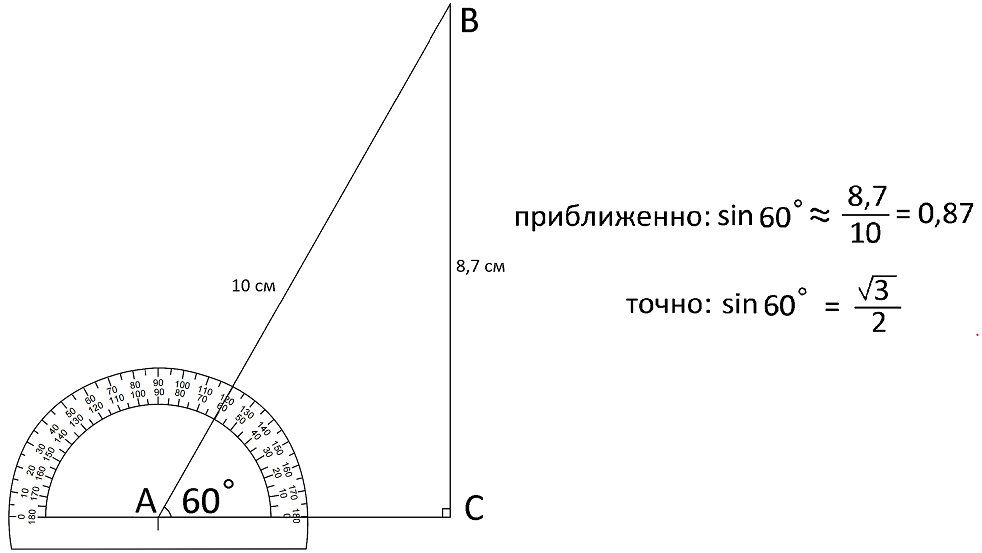
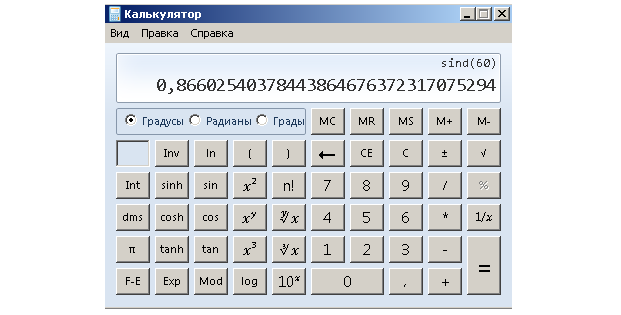
И синус 60° вычислен правильно: наши вычисления и показания калькулятора очень близки.

Косинус

С синусом вроде бы все. Теперь нужно разобраться с косинусом. Формальное определение косинуса:

В силу простой симметрии косинус очень похож на синус - надо только делить на сторону АВ не противолежащую сторону BC, а прилежащую к углу А сторону АС. Определим приближенно косинус 30°: делим длину стороны АС=8,7 см на длину стороны АВ=10 см - получим косинус 30° будет около 0,87. Разумеется косинус тоже не изменится, если взять треугольник с другими сторонами, но с такими же углами: можно было бы начертить треугольник, где сторона АС была бы равна 9 см, а сторона АВ - 10,4 см, так как если 9 разделить 10,4, то получится число очень похожее на 0,87.

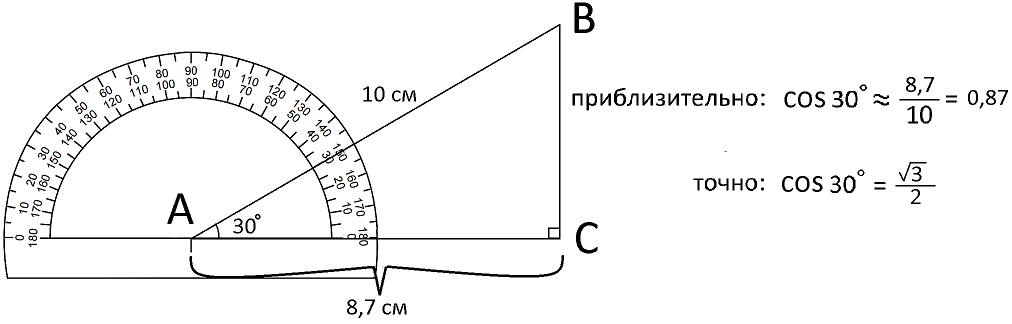
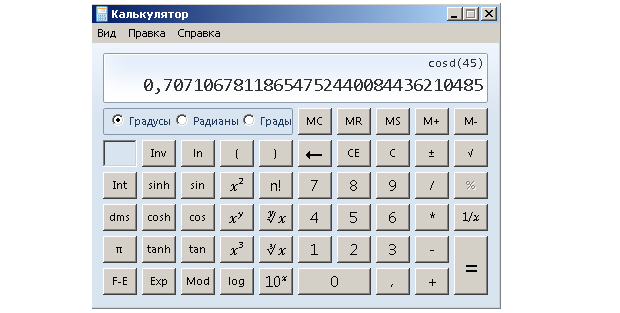
Как вычислить приближенно cos 45° изображено на следующем рисунке.

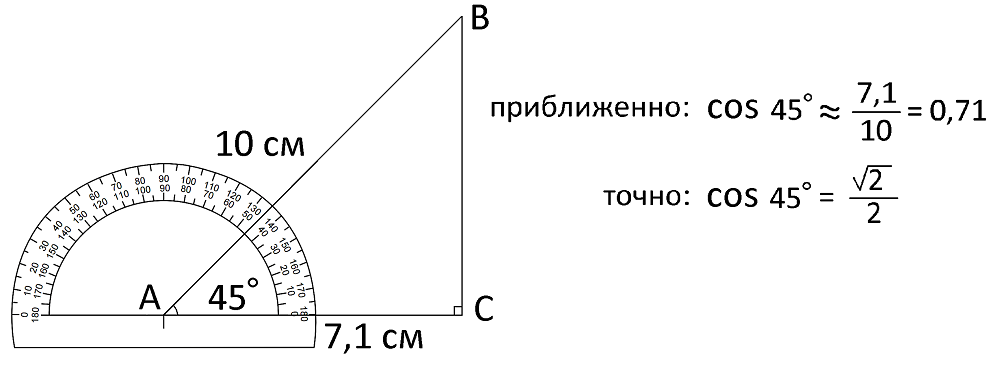
Проверим полученный результат на калькуляторе.

Попробуем вычислить cos 60°

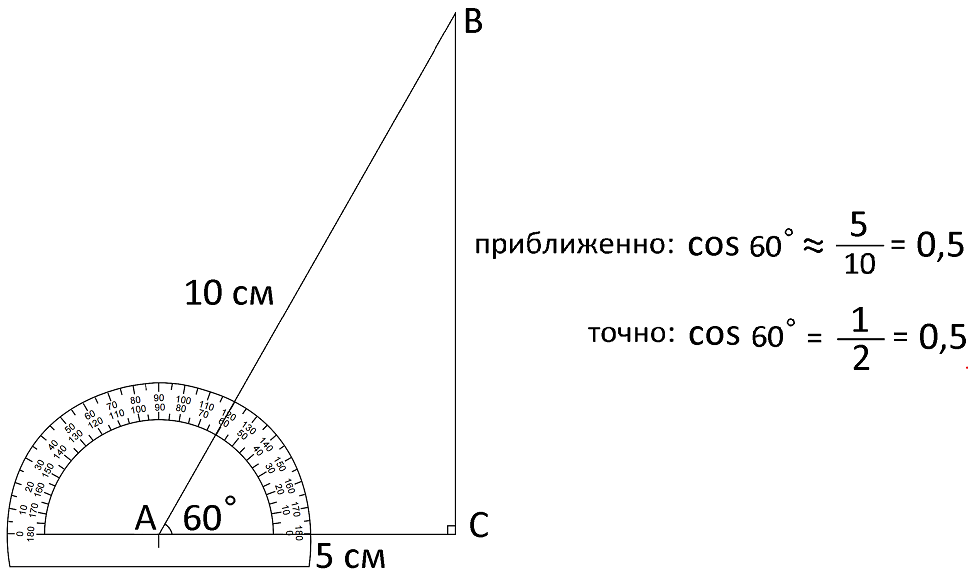
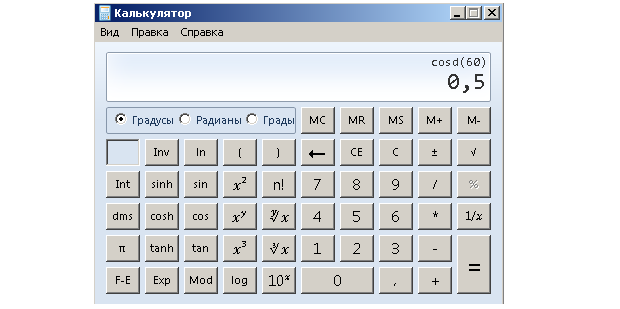
Здесь cos 60° на калькуляторе полностью совпал с нашим результатом. Действительно, всегда, когда в прямоугольном треугольнике есть угол 30° или 60°, катет, лежащий напротив угла 30°, будет равен половине гипотенузы (этот же катет будет являться прилежащим к углу 60°), поэтому sin 30° и cos 60° всегда будут равны 0.5.

Все точные значения синуса и косинуса, которые следует знать указаны в следующей таблице.

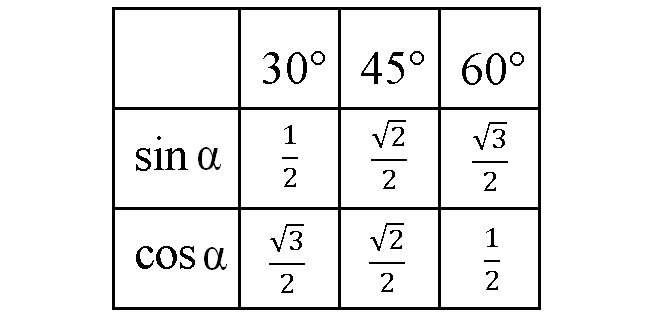
Надеюсь, что удалось понять почему синус и косинус 45° оказались одинаковыми.

© Кирилл Морковкин & Машка Кулибякина