Формулы сокращенного умножения
zhuvalka.ru
Главная / i / t

Формулы сокращенного умножения

Раскрывать скобки в таких выражениях довольно просто:

(x∙y)2 = (x∙y)∙(x∙y) = x∙x∙y∙y = x2∙y2

(x/y)^2 = (x/y)∙(x/y) = (x∙x)/(y∙y) = x^2/y^2

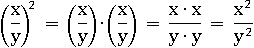
Это быстро можно сделать в случае, когда выражение в скобках содержит только операции умножения или деления. Но гораздо больше требуется промежуточных действий, чтобы раскрыть скобки с выражением, содержащим сумму или разницу двух чисел:

(x + y)2

(x − y)2

И чтобы избавиться от многократного повторения одних и тех же процедур существуют вот такие формулы сокращенного умножения:

Формулы сокращенного умножения

(x + y)2 = x2 + 2∙x∙y + y2

(x − y)2 = x2 − 2∙x∙y + y2

x2 − y2 = (x + y)∙(x − y)

x3 + y3 = (x + y)∙(x2 − x∙y + y2 )

x3 − y3 = (x − y)∙(x2 + x∙y + y2 )

(x + y)3 = x3 + 3∙x2∙y + 3∙x∙y2 + y3

(x − y)3 = x3 − 3∙x2∙y + 3∙x∙y2 − y3

Разберемся по порядку с каждой из этих формул.

Квадрат суммы

Возведем в квадрат следующее выражение:

(x + y)2

Квадратом числа называется умноженное дважды на само себя это число. В нашем случае в квадрат возведено число x+y, значит:

(x + y)2 = (x + y)∙(x + y)

Раскроем скобки:

(x + y)∙(x + y) = x∙x + x∙y + y∙x + y∙y

Дважды умноженный сам на себя x заменим на x2, аналогично заменим и y∙y на y2:

x∙x + x∙y + y∙x + y∙y = x2 + x∙y + y∙x + y2

Числа x∙y и y∙x всегда будут равны друг другу при совершенно любых x и y, поэтому вместо них можно оставить только число x∙y, умноженное на два:

x2 + x∙y + y∙x + y2 = x2 + 2∙x∙y + y2

Ни одно из всех этих преобразований не должно изменить значения первоначального выражения, значит, оно равно конечному:

(x + y)2 = x2 + 2∙x∙y + y2

Это формула сокращенного умножения называется «квадрат суммы».

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(x + y)2 = x2 + 2∙x∙y + y2

Благодаря этой формуле нам теперь не придется многократно выполнять все вышеописанные процедуры.

Данное равенство будет выполняться при абсолютно любых x и y, такие выражения называются тождествами.

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Проверим сохранится ли равенство, если подставить в первую часть формулы вместо x число 3, а вместо y число 5:

(x + y)2 = (3 + 5)2 = 82 = 8∙8 = 64

Подставим эти же числа во вторую часть – будет тоже 64:

x2 + 2∙x∙y + y2 = 32 + 2∙3∙5 + 52 = 9 + 30 + 25 = 64

Равенство сохранилось – обе части равны друг другу.

Причину этой закономерности можно еще объяснить следующей геометрической иллюстрацией.

64 квадратика

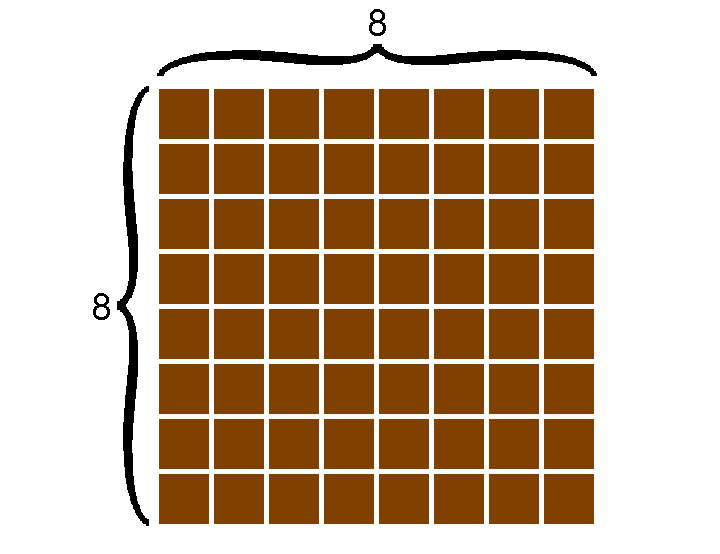
На рисунке изображен большой квадрат 8 на 8, состоящий из 8–ми рядов маленьких квадратиков, и каждый ряд состоит из 8–ми квадратиков. Чтобы посчитать количество маленьких квадратиков достаточно умножить 8 на 8:

8∙8 = 82

В этом выражении можно 8 поменять на 3+5, и посчитать количество квадратиков так:

(3 + 5)2 = 64

Но количество маленьких квадратиков можно посчитать и по-другому: сложить количество красных, зеленых и желтых квадратиков.

9 - красных, 25 - зеленых и 30 - желтых

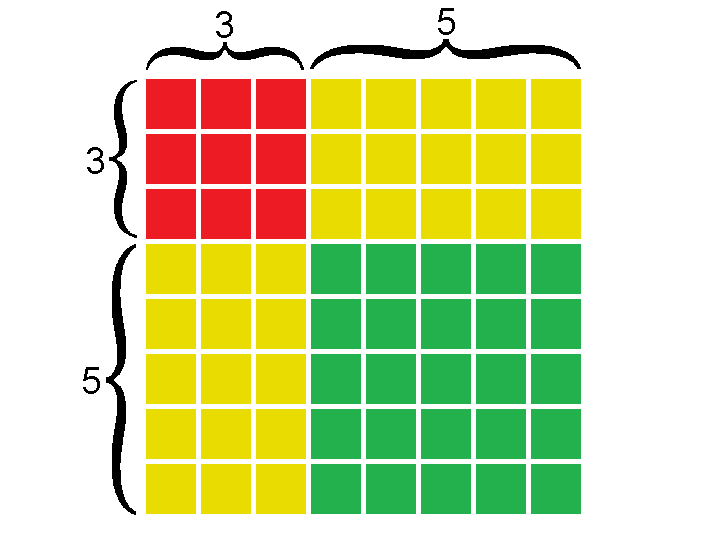
Чтобы посчитать количество красных квадратиков, нужно 3 умножить на 3:

3∙3 = 32 = 9

Количество зеленых вычислим так:

5∙5 = 52 = 25

Каждый из двух желтых прямоугольников состоит из 3 – х рядов, в каждом из которых 5 квадратиков, значит, количество желтых квадратиков можно определить так:

2∙3∙5 = 30

Сложим количество красных, зеленых и желтых квадратиков – получим тоже 64:

32 + 2∙3∙5 + 52 = 9 + 30 + 25 = 64

Очевидно, что оба способа подсчета квадратиков приведут к одному результату 64, значит:

(3 + 5)2 = 32 + 2∙3∙5 + 52

Первая часть этого выражения равна количеству квадратиков, которое подсчитано первым способом, вторая часть равна количеству квадратиков, которое подсчитано вторым способом.

С любыми другими числами равенство также будет всегда выполняться: например, пусть x=9, y=1, тогда:

(x + y)2 = (9 + 1)2 = 102 = 10∙10 = 100

x2 + 2∙x∙y + y2 = 92 + 2∙9∙1 + 12 = 81 + 18 + 1 = 100

Если одно из чисел равно нулю, равенство тоже сохранится: x=7, y=0

(x + y)2 = (7 + 0)2 = 72 = 7∙7 = 49

x2 + 2∙x∙y + y2 = 72 + 2∙7∙0 + 02 = 49 + 0 + 0 = 49

Как видите, это равенство верно при всех допустимых значениях.

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

(x − y)2 = x2 − 2∙x∙y + y2

Это тождество очень похоже на предыдущее. Чтоб убедиться, что это действительно тождество достаточно просто раскрыть скобки:

(x − y)2 = (x − y)∙(x − y)

(x − y)∙(x − y) = x2 − x∙y − y∙x + y2

С полной уверенностью можно заменить −x∙y−y∙x на −2∙x∙y, ибо это одно и то же:

x2 − x∙y − y∙x + y2 = x2 − 2∙x∙y + y2

И из первой части тождества получилась вторая, следовательно, это равенство верно для любых x и y:

Обе части этого тождества будут равны, даже когда x и y – дроби.

Пусть 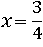x=3/4, y=2/5:

(x − y)^2 = (3/4 − 2/5)^2 =

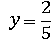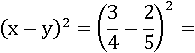
Приведем дроби к общему знаменателю, чтобы отнять одну дробь от другой и возвести в квадрат:

((3∙5)/(4∙5) − (2∙4)/(5∙4))^2 = (15/20 − 8/20)^2 = (7/20)^2 = 49/400 = 0.1225

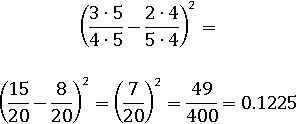
А сейчас сделаем то же самое только уже через формулу:

(3/4 − 2/5)^2 = (3/4)^2 − 2∙(3/4)∙(2/5) + (2/5)^2 = 9/16 − 3/5 + 4/25=

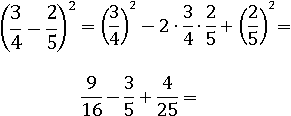
Домножим все дроби, чтоб знаменатель был одинаковый и сложим их:

(9∙25)/(16∙25) − (3∙80)/(5∙80) + (4∙16)/(25∙16) = (9∙25 − 3∙80 + 4∙16)/400 = 49/400 = 0.1225

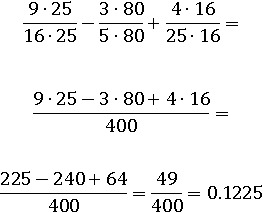
Пример

Упростить выражение:

(3∙a − b)2 + 6∙a∙b − b2

Воспользуемся формулой сокращенного умножения, чтобы раскрыть скобку:

(3∙a − b)2 + 6∙a∙b − b2 =

(3∙a)2 − 2∙3∙a∙b + b2 + 6∙a∙b − b2

Возведем в квадрат 3∙a и заменим 2∙3 на 6:

9∙a2 − 6∙a∙b + b2 + 6∙a∙b − b2

Чтобы было легче заметить, что делать дальше переставим похожие слагаемые поближе друг к другу:

9∙a2 − 6∙a∙b + 6∙a∙b + b2 − b2

Число −6∙a∙b+6∙a∙b при всех a и b будет равна нулю, как и число b2−b2, значит, их можно сократить:

9∙a2 + 6∙a∙b − 6∙a∙b + b2 − b2 = 9∙a2

Выражение стало намного проще – и теперь громоздкая изначальная конструкция равносильна 9∙a2:

(3∙a − b)2 + 6∙a∙b − b2 = 9∙a2

Пусть a=5, b=7, тогда значение первоначального выражения равно 225:

(3∙a − b)2 + 6∙a∙b − b2 =

(3∙5 − 7)2 + 6∙5∙7 − 72 =

=(15 − 7)2 + 210 − 49 =

82 + 210 − 49 = 64 + 210 − 49 = 225

Но у нас есть упрощенная версия того же выражения, и мы можем получить то же число 225 гораздо легче:

9∙a2 = 9∙52 = 9∙5∙5 = 225

Отсутствие числа b в выражении 9∙a2 означает, что от b ничего не зависит – попробуйте в первоначальном выражении число a оставить равным пяти, а вместо b подставьте любое другое число – получится тоже 225.

Разность квадратов

Еще одна очень популярная формула сокращенного умножения – «разность квадратов»:

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

x2 − y2 = (x + y)∙(x − y)

Доказать это тождество очень легко:

(x + y)∙(x − y) = x∙x − x∙y + y∙x − y∙y =

x2 − x∙y + y∙x − y2 =

Сумма −x∙y+y∙x всегда будет равна нулю, какие числа вместо x и y мы бы ни подставляли, поэтому их можно просто убрать – от этого ничего не изменится:

x2 − x∙y + y∙x − y2 = x2 − y2

Проверим справедливость этого тождества:

Пусть x=124, y=123

(x + y)∙(x − y) = (124 + 123)∙(124 − 123) = 247∙1 = 247

x2 − y2 = 1242 − 1232 = 15376 − 15129 = 247

Вычисления в первом случае гораздо легче, чем во втором, поэтому, вместо вычисления значения выражения 1242 − 1232, иногда вычисляют значение выражения (124+123)∙(124 − 123).

Пример

Упростить выражение:

(x^2 − 9)/(x + 3)

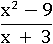
Чтобы в числителе появилась разность квадратов двух чисел, нужно заменить 9 на 32:

(x^2 − 3^2)/(x + 3)=

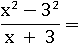
Теперь можно применить формулу:

((x + 3)∙(x − 3))/(x + 3)=

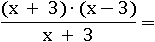
Разделим числитель и знаменатель на число x+3, основное свойство дроби говорит, что от этого дробь не изменит значения:

((x + 3)∙(x − 3))/(x + 3) = ((x − 3))/1 = x − 3

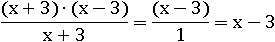
Но обязательно следует учитывать, что до сокращения на x + 3, вместо x нельзя было подставить − 3 (будет деление на ноль), а после – уже можно. Поэтому сокращение на выражение, содержащее переменную, не всегда приводит к абсолютно тождественному выражению. В нашем случае первоначальное выражение тождественно конечному для всех x кроме случая, когда x = −3:

(x^2 − 9)/(x + 3) = x − 3         x ≠ −3

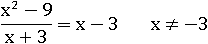
Подставим 100 вместо x в первое неупрощенное выражение – получим 97:

(x^2 − 9)/(x + 3) = (100^2 − 9)/(100 + 3) = (10000 − 9)/103 = 9991/103 = 97

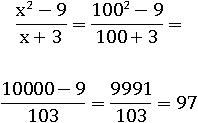
И подставим в упрощенное:

x − 3 = 100 − 3 = 97

Очевидно, что с упрощенным выражением легче работать чем с первоначальным.

Сумма кубов

Все следующие формулы используются гораздо реже чем предыдущие, но иногда они незаменимы.

Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности:

x3 + y3 = (x + y)∙(x2 − x∙y + y2)

Раскроем скобки второй части этого тождества:

(x + y)∙(x2 − x∙y + y2) = x3 − x2∙y + x∙y2 + x2∙y − x∙y2 + y3

Сумма –x2∙y+x∙y2+x2∙y–x∙y2 равна нулю, уберем эту сумму, тогда из второй части тождества получится первая:

x3 + y3

Теперь проверим равенство на числах:

Пусть x=5, y=2

x3 + y3 = 53 + 23 = 125 + 8 = 133

Вторая часть тождетсва тоже будет равна 133:

(x + y)∙(x2 − x∙y + y2) =

(5 + 2)∙(52 − 5∙2 + 22 ) =

(7)∙(25 − 10 + 4) = 7∙19 = 133

Пример

Упростить выражение:

(x^3 + 125)/(x^2 − 5∙x + 25)

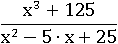
Число 125 равно числу 53, а 25=52, тогда их можно заменить:

(x^3 + 5^3)/(x^2 − 5∙x + 5^2) =

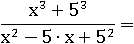
В числителе появилась разница кубов, значит можно применить формулу:

((x + 5)∙(x^2 − x∙5 + 5^2))/(x^2 − 5∙x + 5^2) =

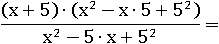
Воспользуемся основным свойством дроби, чтобы сократить дробь:

(x + 5)/1 = x + 5

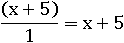
Так как знаменатель x2 − 5∙x + 52 ни при одном действительном x никогда не будет равен нулю, то можно совершенно спокойно его сокращать, не беспокоясь за потерю равносильности.

Теперь при x=7, значение этого выражения можно вычислить так:

(7^3 + 125)/(7^2 − 5∙7 + 25) = 12

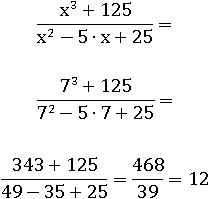
Но поскольку мы уже упростили это выражение, то тот же результат можно получить так:

x + 5 = 7 + 5 = 12

Разность кубов

Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы:

x3 − y3 = (x − y)∙(x2 + x∙y + y2)

Докажем это тождество:

(x − y)∙(x2 + x∙y + y2) =

x3 + x2∙y + x∙y2 − x2∙y − x∙y2 − y3 =

Сократим слагаемые, сумма которых равна нулю:

x3 + x2∙y + x∙y2 − x2∙y − x∙y2 − y3 =

x3 + y3

Аналогично убедимся в равенстве на тех же числах: x=5, y=3

x3 − y3 = 53 − 33 = 125 − 27 = 98

(x + y)∙(x2 − x∙y + y2) =

(5 − 3)∙(52 + 5∙3 + 32) =

(2)∙(25 + 15 + 9) = 2∙49 = 98

Куб суммы

Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, плюс куб второго числа

(x + y)3 = x3 + 3∙x2∙y + 3∙x∙y2 + y3

Чтобы доказать эту формулу нам потребуется сначала применить первое свойство степени:

(x + y)3 = (x + y)∙(x + y)2 =

По уже знакомой формуле квадрата суммы заменим вторую скобку:

(x + y)∙(x2 + 2∙x∙y + y2) =

И раскроем скобки по стандартной схеме:

(x + y)∙(x2 + 2∙x∙y + y2) = x3 + 2∙x2∙y + x∙y2 + x2∙y + 2∙x∙y2 + y3 =

Немного переставим слагаемые:

x3 + 2∙x2∙y + x2∙y + x∙y2 + 2∙x∙y2 + y3 =

К удвоенному x2∙y прибавляется одно x2∙y, следовательно, их сумму можно заменить утроенным x2∙y:

x3 + 3∙x2∙y + x∙y2 + 2∙x∙y2 + y3 =

Таким же образом поменяем x∙y2 + 2∙x∙y2 на 3∙x∙y2, которое имеет тот же смысл:

x3 + 3∙x2∙y + 3∙x∙y2 + y3 =

Так что теперь куб суммы можно посчитать не только так: x=6, y=4

(6 + 4)3 = 103 = 1000

Но еще и так:

63 + 3∙62∙4 + 3∙6∙42 + 43 = 216 + 432 + 288 + 64 = 1000

Пример

Упростить выражение:

(∛x + 2)^3 − 6∙(∛x)^2 − 12∙∛x − 7

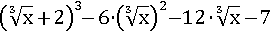
Раскроем скобку в кубе по формуле:

(∛x)^3 + 3∙(∛x)^2∙2 + 3∙∛x∙2^2 + 2^3 − 6∙(∛x)^2 − 12∙∛x − 7

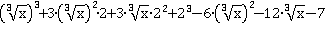
Заменим 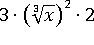3∙((∛x)^2)∙2 на равное ему 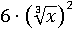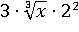6∙((∛x)^2), 3∙(∛x)∙2^2 заменим на 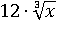12∙∛x, а 23 на 8:

(∛x)^3 + 6∙(∛x)^2 + 12∙∛x + 8 − 6∙(∛x)^2 − 12∙∛x − 7=

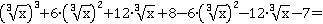
Убираем слагаемые, сумма которых равна нулю, и потому никак не влияет на значение выражения:

(∛x)^3 + 8 − 7=

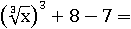
Заменим 8 − 7 на 1:

(∛x)^3 + 1 =

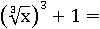
По определению корня 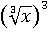(∛x)^3 равен x, значит:

x + 1

Оказывается, что первоначальное сложное выражение равносильно такому простому конечному:

(∛x + 2)^3 − 6∙(∛x)^2 − 12∙∛x − 7 = x + 1

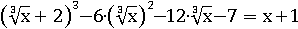
Проверить равносильность выражений можно на совершенно любом числе, например, пусть x будет равен 125, тогда изначальное выражение будет иметь значение 126:

(∛125 + 2)^3 − 6∙(∛125)^2 − 12∙∛125 − 7=

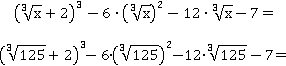
(5 + 2)3 − 6∙(5)2 − 12∙5 − 7 =

(7)3 − 6∙25 − 60 − 7 =

343 − 150 − 60 − 7 = 126

Но вместо всех этих громоздких вычислений значения выражения при x=125 достаточно было воспользоваться его упрощенной версией, в которой просто нужно к 125 прибавить единицу и получить то же значение 126:

x + 1 = 125 + 1 = 126

Куб разности

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(x − y)3 = x3 − 3∙x2∙y + 3∙x∙y2 − y3

Доказательство этой формулы произведем по той же схеме, которая использовалась в предыдущий раз:

(x − y)3 =

(x − y)∙(x2 − 2∙x∙y + y2) =

x3 − 2∙x2∙y + x∙y2 − x2∙y + 2∙x∙y2 − y3 =

x3 − 2∙x2∙y − x2∙y + x∙y2 + 2∙x∙y2 − y3 =

x3 − 3∙x2∙y + x∙y2 + 2∙x∙y2 − y3 =

x3 − 3∙x2∙y + 3∙x∙y2 − y3

Пусть x=6, y=4, тогда куб разности этих чисел будет равен:

(6 − 4)3 = 23 = 8

Если посчитать, предварительно раскрыв скобки по формуле, то получится тоже восемь:

63 − 3∙62∙4 + 3∙6∙42 − 43 = 216 − 432 + 288 − 64 = 8

Увеличенное изображение