Косинус на тригонометрической окружности
В прошлый раз мы узнали, что из себя представляют такие тригонометрические функции как синус, косинус, тангенс и котангенс только для острых (от 0° до 90°) углов, но это значительно поможет тому, чтобы перейти к следующему, более точному, определению тригонометрической функции для любого угла от 0° до 360°.
Нарисуем обычную систему координат, только дополним еще ее окружностью, центр которой находится в точке A, а ее радиус равен единице. Затем проведем луч AB с началом в точке A, пересекающий окружность в точке B. Таким образом у нас получится тригонометрическая окружность (или единичная окружность).
Опустим перпендикуляр из точки B на ось X. И у нас опять образовался прямоугольный треугольник ABC, в котором сторона AB является не только гипотенузой, но и еще радиусом окружности.
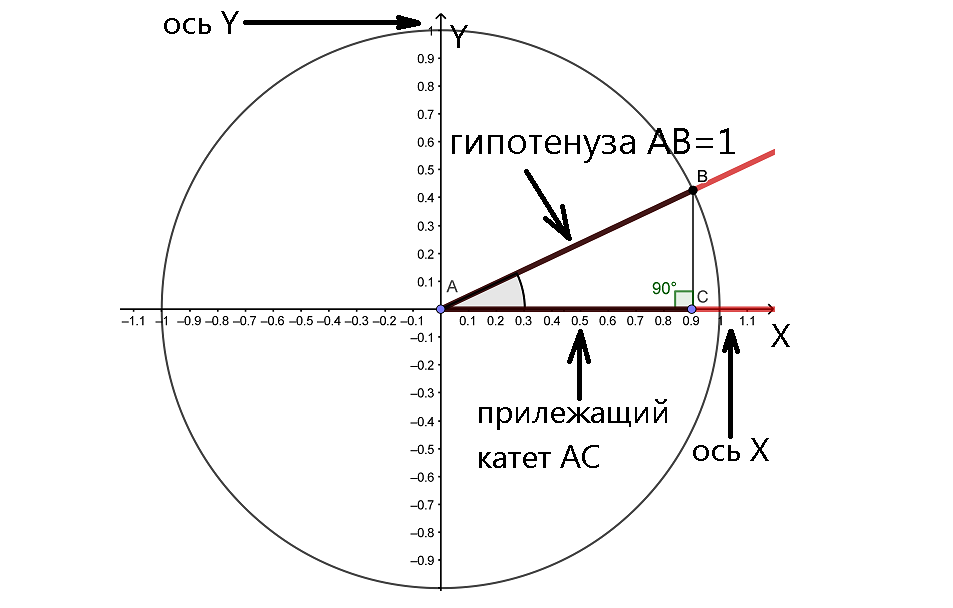
Чтобы вычислить косинус угла, нам понадобится длину прилежащего к углу AC катета поделить на длину гипотенузы AB. Только, в отличие от предыдущего раза, длину катета AC в этот раз не обязательно нужно будет измерять, т.к. длина катета AC будет полностью совпадать с координатой точки C на оси X, поэтому достаточно просто посмотреть какая координата на оси X у точки C. Точка C будет как бы находиться уже на линейке, которой является ось X.
Попробуем определить косинус 60° уже с помощью тригонометрической окружности: по оси X видно, что координата точки C равна 0.5, значит, и длина катета AC тоже равна 0.5. А длина гипотенузы AB является радиусом окружности и всегда (независимо от угла) будет равна 1. Остается только поделить длину AC (или координату точки C) на длину гипотенузы AB, равную 1:
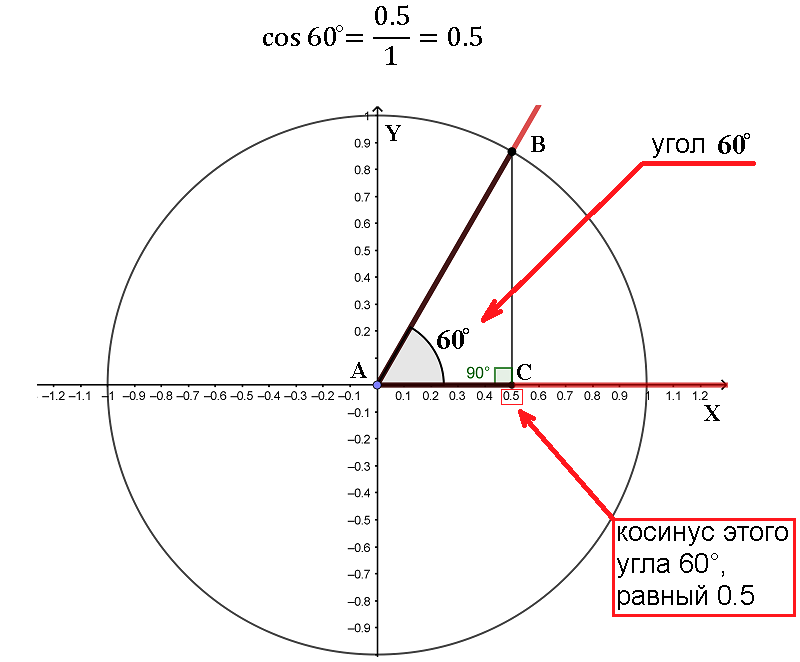
Но при делении на единицу любое число не изменится, значит, можно было бы просто посмотреть на координату точки C на оси X – она и будет являться косинусом 60°. Именно по координате точки C и надо будет теперь всегда определять косинус угла.
A как же определить, чему равен косинус 120°? Невозможно же будет начертить прямоугольный треугольник с углом 120°, т.к. сумма углов в любом треугольнике всегда равна 180°, а в прямоугольном треугольнике с углом 120° сумма только двух углов уже больше 180°: 120°+90°=210°. На следующем рисунке изображена попытка нарисовать такой треугольник.
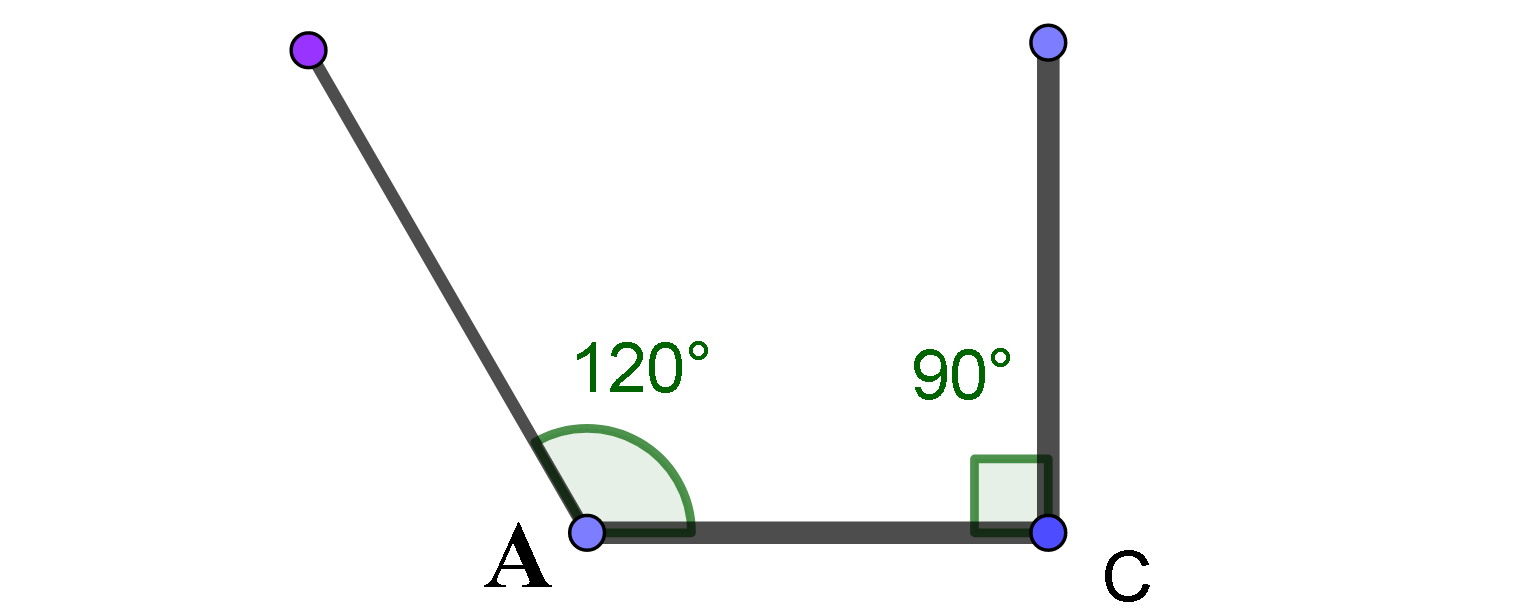
Зато угол 120° можно отмерить в тригонометрической окружности, опустить перпендикуляр BC из точки B на ось X, и тогда координата точки C на оси X будет являться косинусом 120°.
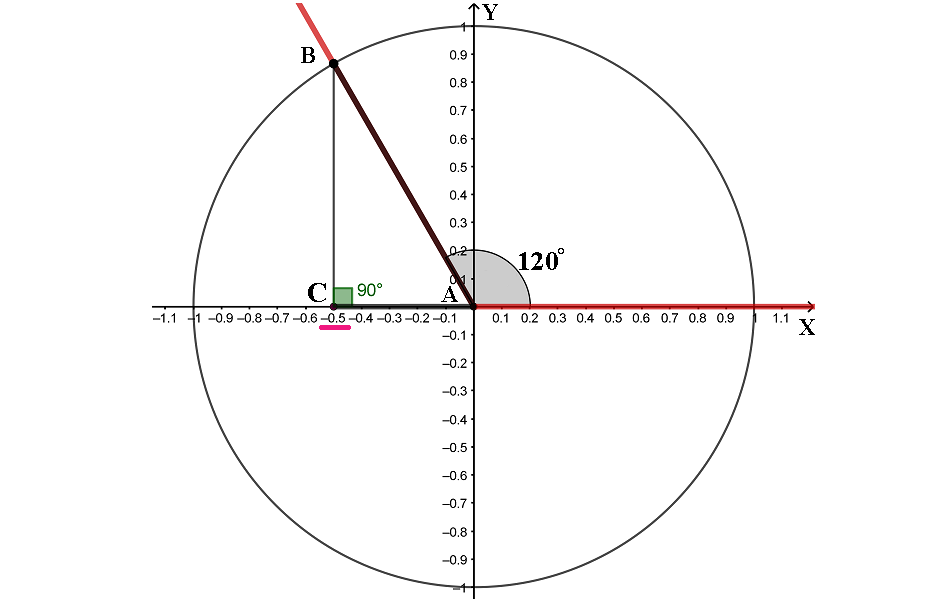
Точка C на оси X разместилась ровно на числе -0.5, значит, cos 120° = -0.5.
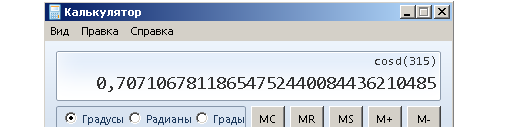
Полученное число -0,5 легко проверить с помощью обычного калькулятора, поставленного в инженерный режим, такой калькулятор легко найти в любом компьютере.
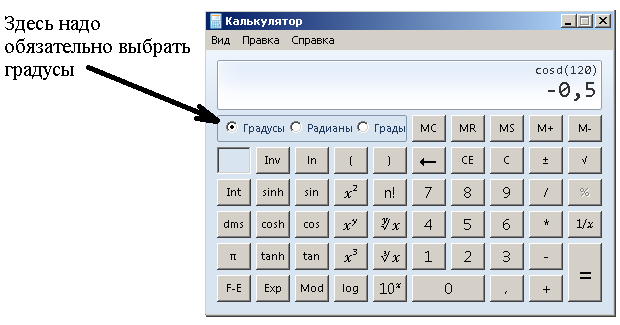
И калькулятор полностью согласен с нами.
Таким образом для приближенного определения косинуса угла α достаточно просто провести луч AB так, чтобы получился нужный угол, опустить перпендикуляр BC из точки B на ось X, и тогда точка C на оси X, как раз и укажет на число равное косинусу этого угла. Более того, теперь угол можно задать абсолютно любой от 0° до 360°.
Для примера попробуем приближенно определить косинус 210°. Отмерим угол 210° на окружности и опустим перпендикуляр BC из точки C на ось X. Точка C встанет где-то на числе -0,87, это значит, что косинус 210° будет приблизительно равен -0,87.
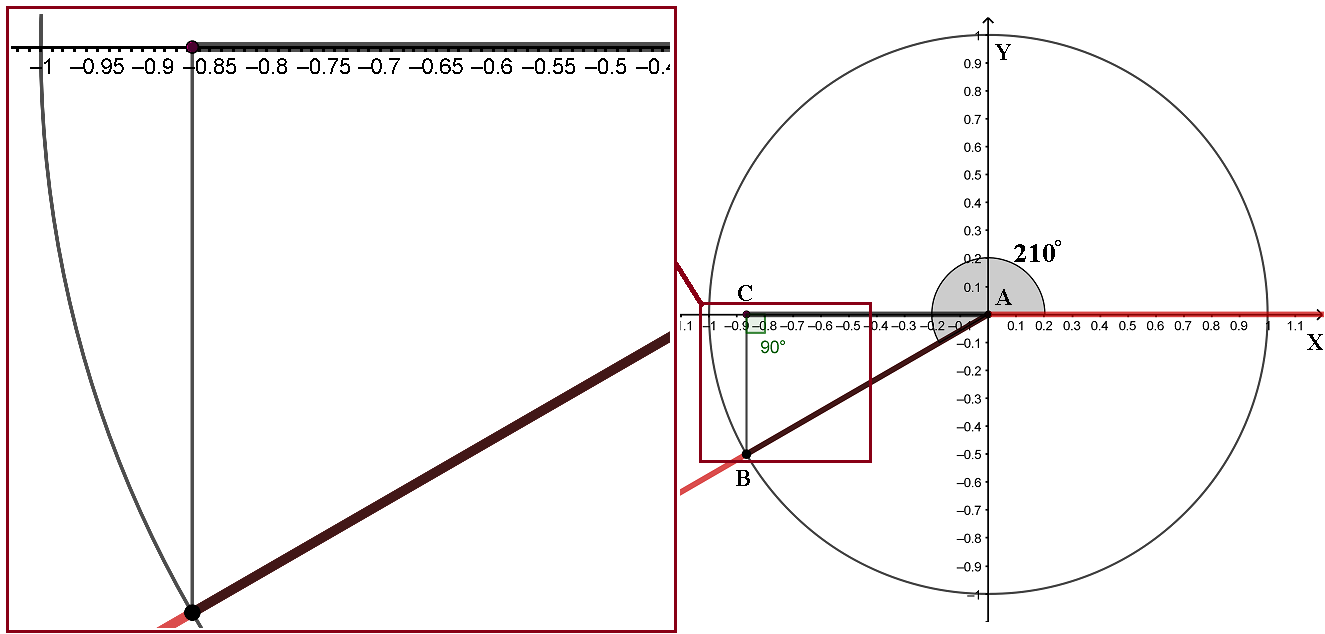
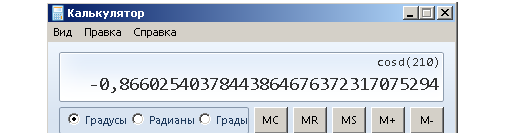
Калькулятор показал нам почти такой же результат (только более точный), следовательно, мы все правильно сделали. Aбсолютно точное же значение косинуса 210° равно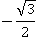 
, это число придется запомнить, но единичная окружность очень сильно облегчает этот процесс (тригонометрическая окружность с точными значениями синуса и косинуса всех основных углов будет приведена ниже).
Далее приведен рисунок с аналогичным примером косинуса 315° на тригонометрической окружности
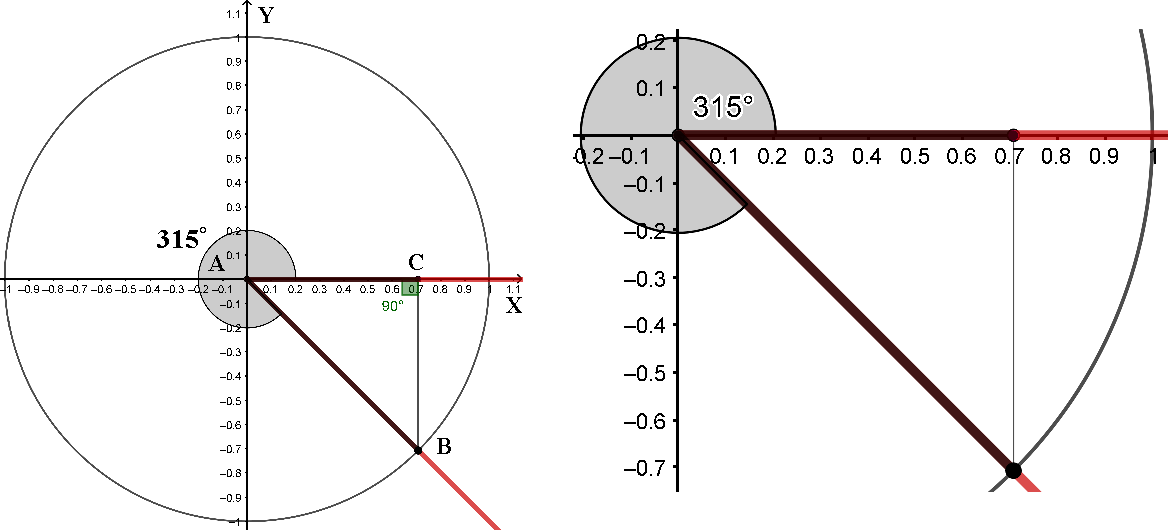
Синус на тригонометрической окружности
С синусом дело обстоит очень похоже. Если пользоваться старым определением то, синус угла A получится, если длину противолежащей углу A стороны BC разделить на длину все той же гипотенузы AB, являющуюся радиусом единичной окружности. То есть деление стороны BC будет осуществляться тоже на единицу, а значит и синус угла A при любом угле всегда будет равен катету BC:
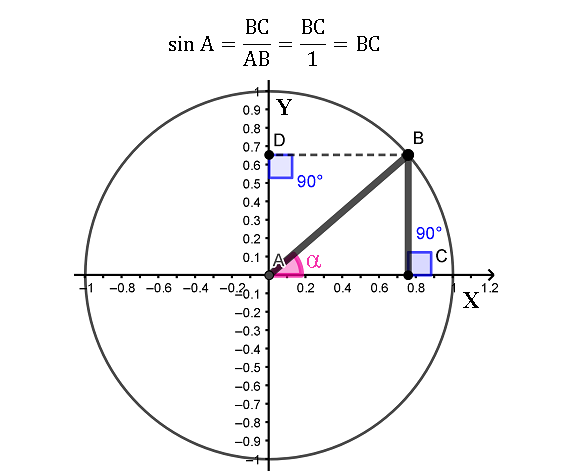
Для удобства угол A обозначим греческой буквой α (читается - «альфа»). Опустим перпендикуляр BD из точки B на ось Y. Легко можно заметить, что отрезок BC будет равен координате точки D на оси Y, тогда синус угла α будет равен не только длине BC и AD, но и координате точки D:
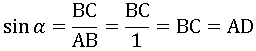
Координатой точки D будет гораздо удобнее пользоваться в будущем, нежели отрезком BC.
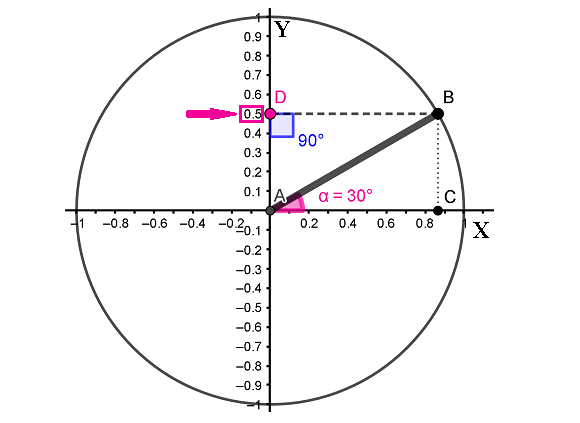
Получается, что при любом угле α sin α будет равен координате точки D на оси Y. Например, что синус 30° равен 0.5, гораздо легче заметить на тригонометрической окружности по координате точки D на оси Y.
A теперь попробуем приближенно определить синус 135°: отмерим на окружности угол 135°, проведем луч AB и опустим перпендикуляр BD из точки B на осьY, тогда точка D укажет на число, близкое к 0,71 на оси Y, значит, синус 135° приблизительно равен 0,71 (точно: sin 135° =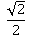 
).
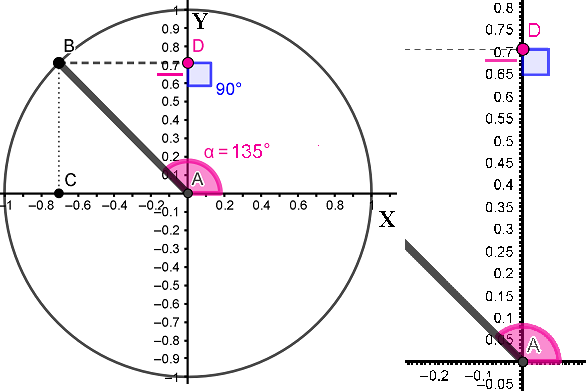
Точно таким же образом на следующих рисунках даны примеры определения sin 240°, sin 330° и сравнение этих результатов с калькулятором.
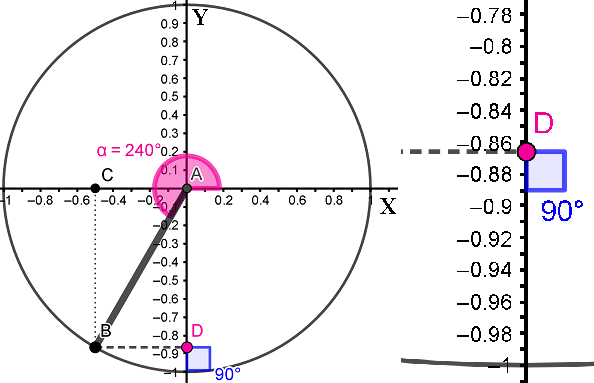
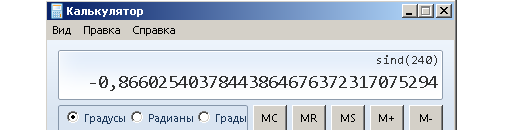
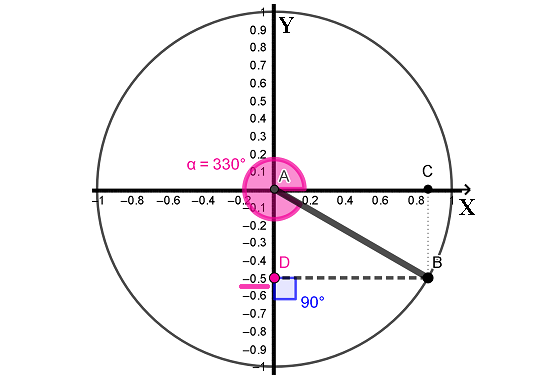
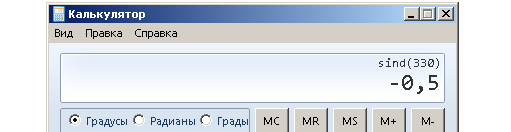
Обобщим сказанное:
Для определения синуса или косинуса угла нужно взять соответствующую этому углу точку на тригонометрической окружности, и тогда координата X этой точки будет равна косинусу этого угла, а координата Y будет равна синусу этого угла.
Точные синусы и косинусы всех основных (школьных) углов изображены на следующем рисунке.
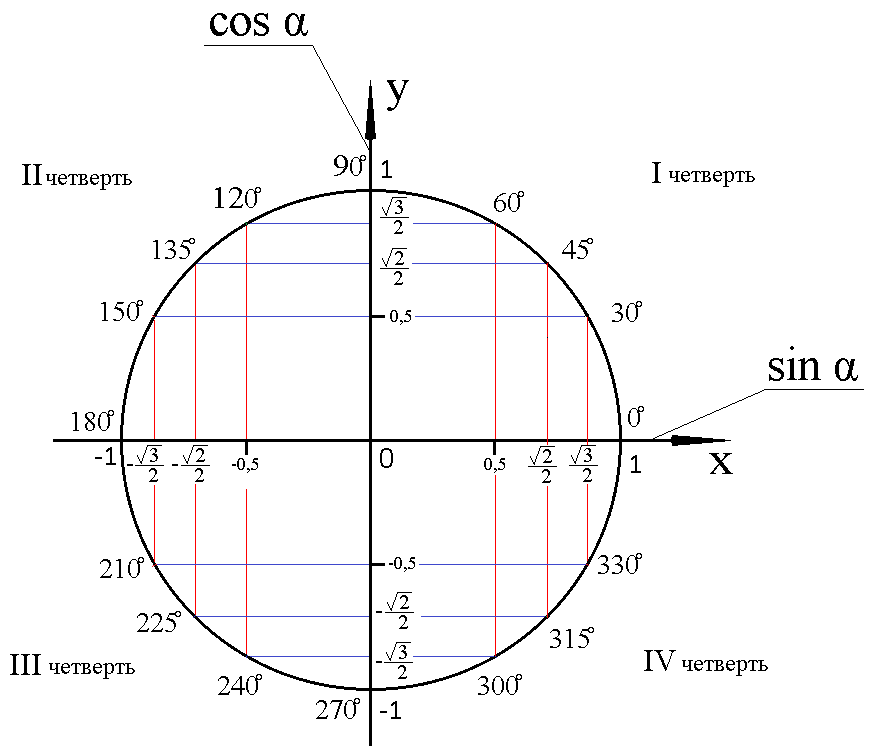
Определим по этой окружности sin 300° и cos 300°. Находим на окружности точку 300° (зеленая точка), строим перпендикуляр (красная жирная линия) из этой точки на ось X, и он покажет на число 0.5, следовательно, cos 300°= 0.5. Строим перпендикуляр (синяя жирная линия) из зеленой точки на ось Y, и видим, что перпендикуляр покажет на число 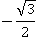, значит sin 300° = .
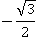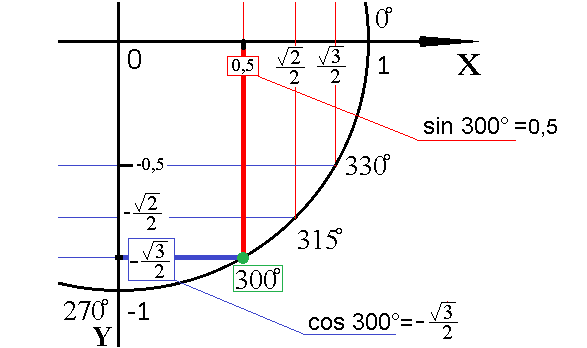
Следует заметить, что на тригонометрической окружности есть некие особые углы такие как 90°, 180°, 270° и 360°. Если отмерить угол 90 и опустить перпендикуляр BC из точки B на ось X, то точка C сольется с точкой A и на оси окажется точно на нуле т.е. cos 90°=0.
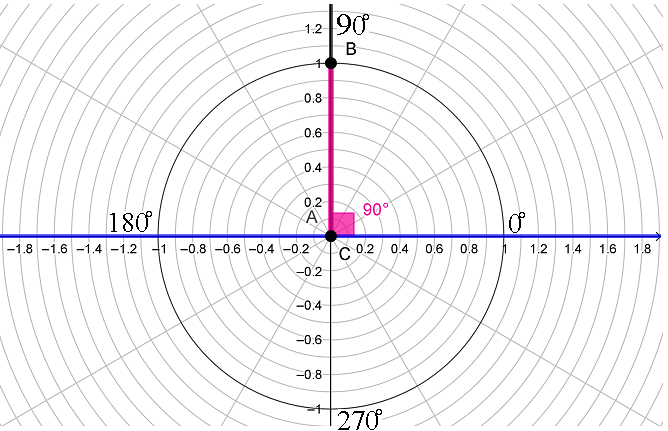
Если точку B на тригонометрической окружности плавно перемещать от 0° до 90°, и при этом следить за координатой точки B, то будет заметно, что по мере приближения угла к 90° координата точки D на оси Y возрастает и приближается к 1. Значит, когда угол α станет равным 90°, то синус α будет равным 1, таким образом, sin 90°=1.
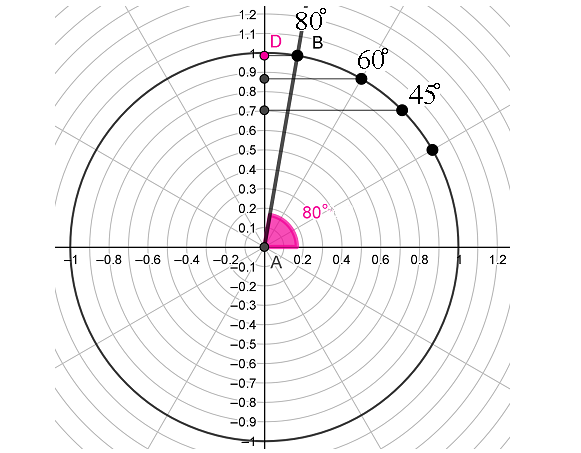
Рассуждая аналогичным образом, с помощью тригонометрической окружности можно легко установить следующее:
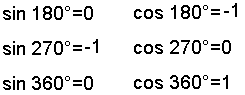
Для лучшего усвоения следует это проверить это самостоятельно.