Что такое функция
Определение
Чтобы было проще понять что такое функция, сначала разберем такой пример.
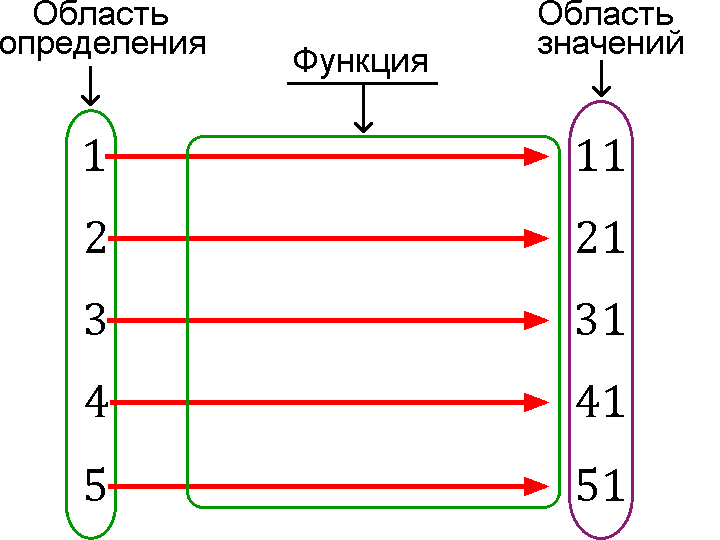
Пусть есть множество X, состоящее из пяти натуральных чисел от 1 до 5, вот все элементы этого множества:
X = {1, 2, 3, 4, 5}
Теперь возьмем из множества X какое-нибудь число, например 1, умножим его на 10 и к тому, что получится, прибавим 1:
10∙1+1=11
Это число 11 поставим в соответствие числу 1, которое брали из множества X:
1⟶11
Таким же образом можно поступить с любым другим числом из множества X. Возьмем число 2 из множества X, и применим к нему то же самое правило: умножим его на 10 и прибавим 1:
10∙2+1=21
Тогда числу 2 из X, к которому применяли правило, будет соответствовать число 21:
2⟶21
С числом 3 из множества X поступим аналогично – умножим на 10 и прибавим 1:
10∙3+1=31
И сопоставим числу 3 из X число 31:
3⟶31
Применим это правило к оставшимся числам 4 и 5 из множества X – получим еще числа 41 и 51:
10∙4+1=41
10∙5+1=51
И сделаем еще два соответствия:
4⟶41
5⟶51
Множество из пяти чисел, которое получилось в результате применения правила, назовем буквой Y:
Y = {11, 21, 31, 41, 51}
Правило, по которому можно, по числу из множества X, получить соответствующее ему число из множества Y называется функцией. В нашем случае функцией является правило, в котором мы число из X умножали на 10 и прибавляли 1.
Функции можно описывать (задавать) самыми разными способами, например, просто перечислением всех соответствий, если их конечное количество:
1⟶11
2⟶21
3⟶31
4⟶41
5⟶51
В виде таблицы:
| X | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Y | 11 | 21 | 31 | 41 | 51 |
Просто словами: «существует множество X с натуральными числами от 1 до 5. Чтобы по числу из множества X получить соответствующее ему число из множества Y, нужно число из множества X умножить на 10 и прибавить 1».
Функцию можно задать в виде графика (об этом способе речь пойдет в следующих статьях)
Но обычно функцию задают с помощью формулы, в таком случае говорят, что функция задана аналитически. Нашу функцию можно задать такой формулой:
y = 10∙x+1
Как уже известно, в нашей функции числу 3 из множества X соответствует число 31 из Y, это же соответствие можно установить и с помощью этой формулы, если вместо x подставить число 3, то y будет равен 31:
y = 10∙3+1 = 30+1 = 31
Так можно установить соответствие каждому элементу из X. Например, числу 4 из X соответствует число 41 из множества Y и формула показывает такое же соответствие:
y = 10∙4+1 = 40+1 = 41
В таких случаях говорят, что число 41 является значением функции при x = 4 или значение функции в точке x=4 равно 41.
В точке x = 5 значение функции будет равно 51:
y = 10∙5+1 = 50+1 = 51
Переменные x и y в формуле этой функции неравноправны, x – независимая переменная, которую еще называют аргументом, y – зависимая переменная, так как ее значение зависит от x. Стрелки на рисунках, изображающих функцию, всегда идут от значения независимой переменной к значению зависимой. Саму же функцию иногда называют зависимостью.
Независимую переменную чаще обозначают буквой x, зависимую – буквой y, но на самом деле их можно обозначать любыми буквами.
Множество, в которое входят все значения независимой переменной, называют областью определения функции, а множество, в которое входят все значения зависимой переменной, – областью значений функции. В функции y = 2∙x+1 областью определения было множество X:
X = {1, 2, 3, 4, 5}
А областью значений – множество Y:
Y = {11, 21, 31, 41, 51}
Количество чисел в области определения и области значений может быть каким угодно, в том числе и бесконечным, как и в большинстве школьных функций. В следующих статьях мы еще не раз будем встречаться с такими понятиями как область определения и область значений и разберем их более детально.
Разумеется y = 10∙x+1 – не единственная функция с такой областью определения и областью значений. Можно придумать новую функцию, которая будет тем же числам из X ставить в соответствие такие же числа из Y, но по другому правилу, например, такую:
y = 61−10∙x
Новая функция числу 1 будет ставить в соответствие уже число 51:
y = 61−10∙1 = 61−10 = 51
А числу 2 – число 41 из множества Y:
y = 61−10∙2 = 61−20 = 41
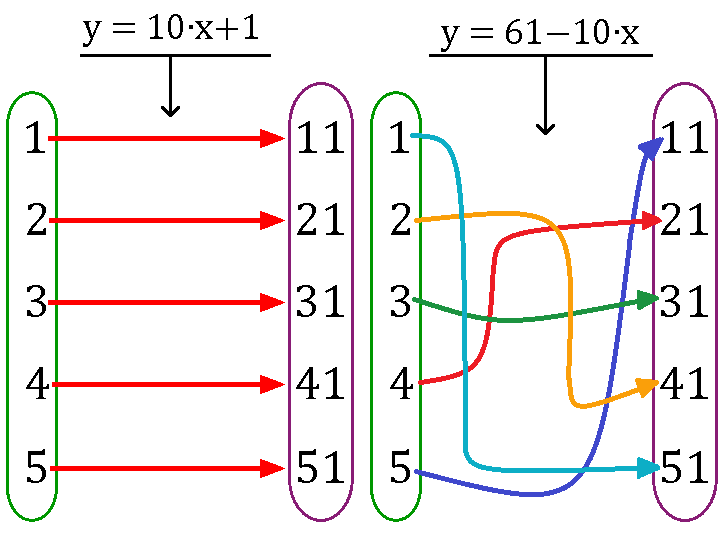
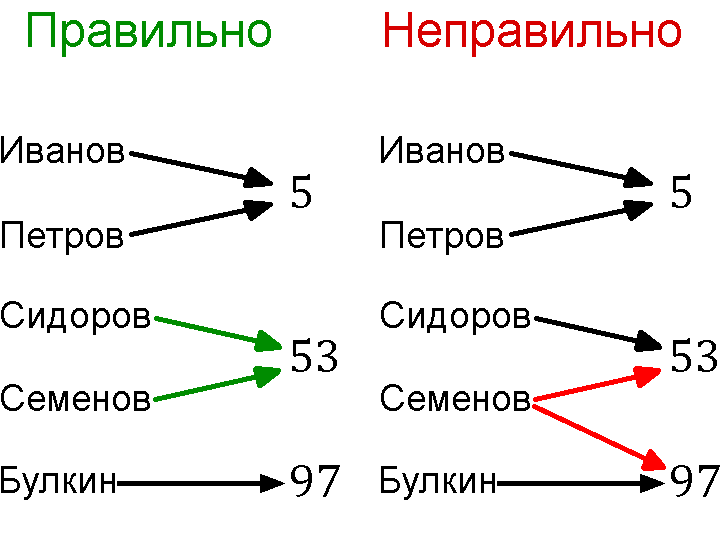
Еще одна важная деталь: функция должна какому-либо значению независимой переменной ставить в соответствие только одно значение зависимой переменной. То есть неважно, какое число из области определения мы подставим вместо x в формулу, y обязан принять единственное возможное значение.
Однако, допускается, чтобы функция нескольким значениям независимой переменной ставила в соответствие одно и то же значение зависимой переменной. Например, при разных значениях x эта функция принимает одинаковые значения:
y = (x−3)2
В точке x = 1 и в точке x = 5 оба значения равны четырем:
y = (1−3)2 = (−2)2 = 4
y = (5−3)2=22 = 4
Зададим функцию, которая будет фамилии человека ставить в соответствие его возраст. Область определения – это множество фамилий, область значений – множество возрастов этих людей. Тогда некоторые разные люди могут иметь одинаковый возраст, но один и тот же человек не может иметь хотя бы два разных возраста.
Теперь можно дать точное определение, сейчас оно должно быть полностью понятным:
Функция – это правило, по которому каждому элементу из первого множества (области определения) ставится в соответствие единственный элемент из второго множества (области значений).
Очевидно, что в этом определении элементы из первого множества будут обозначаться независимой переменной (аргумент), а элементы из второго – зависимой.
Перейдем к конкретному примеру.
Пример
В некоторых странах для измерения температуры пользуются шкалой Фаренгейта, а не Цельсия как у нас. Выходит, что одна и та же температура будет иметь разные численные обозначения в разных единицах измерения. Например, температура кипения воды при нормальных условиях равна 100° по Цельсию, а в градусах Фаренгейта эта же температура кипения воды равна 212°. Существует функция, с помощью которой можно легко вычислить какая температура по Фаренгейту соответствует данной температуре по Цельсию:
F = 1.8∙C+32
Для более удобного перевода из шкалы Цельсия в шкалу Фаренгейта, независимой переменной будем считать C – температуру по Цельсию, зависимой – F – температуру по Фаренгейту.
Чтобы узнать, какая температура по Фаренгейту соответствует нулю градусов по Цельсию, нужно вместо буквы C подставить ноль в формулу функции. Так температуре 0° по Цельсию соответствует температура +32° по Фаренгейту:
F = 1.8∙C+32 = 1.8∙0+32 = 32
Если на термометре со шкалой Цельсия будет температура +20°, то, стоящий рядом, термометр со шкалой Фаренгейта покажет +68°:
F = 1.8∙20+32 = 36+32 = 68
А при температуре −40° термометры с разными шкалами уже покажут одинаковую температуру. Это единственный случай, когда температуры на обеих шкалах будут совпадать:
F = 1.8∙(−40)+32 = −72+32 = −40
Областью определения данной функции, пожалуй, можно считать весь диапазон от самой низкой температуры (абсолютный ноль −273,15 °C ) до самой высокой теоретически возможной Планковской температуры (1.41679∙10 32 °C ). Тогда областью значений будет любое число от абсолютного нуля по фаренгейту (−459.67 °F ) до Планковской температуры по Фаренгейту (2.5502∙10 32 °F ).
Частично эту функцию можно задать перечислением нескольких соответствий:
−30°C⟶−22°F 0°C⟶32°F
−20°C⟶−4°F 10°C⟶50°F
−10°C⟶14°F 20°C⟶68°F
Еще можно те же соответствия задать в виде таблицы:
| °C | -40 | -30 | -20 | -10 | 0 | 10 | 20 | 30 |
|---|---|---|---|---|---|---|---|---|
| °F | -40 | -22 | -4 | 14 | 32 | 50 | 68 | 86 |
Но аналитический способ задания этой функции (в виде формулы F = 1.8∙C+32 ) в большинстве случаев гораздо удобнее.
Есть и обратная функция, с помощью которой можно наоборот перевести температуру из шкалы Фаренгейта в шкалу Цельсия. Только независимой переменной будет теперь F:
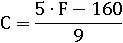
Подставим вместо F температуру по Фаренгейту +68°, и мы получим соответствующую температуру +20° по Цельсию:
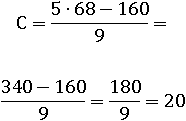
Функции могут быть заданы самыми разнообразными формулами как очень простыми, так и довольно сложными и громоздкими с использованием дробей, степеней, квадратных корней, корней n-й степени:
y = x
y = |x|
y = x2
y = 2x
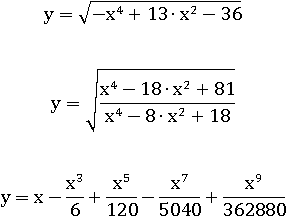
Области определения и области значений всех этих функций состоят из бесконечного количества чисел.
Кусочная функция
Бывает так, что для одних значений независимой переменной функцию задают одной формулой, а для других значений независимой переменной – другой формулой, такие функции называют кусочными; вот пример одной из них:
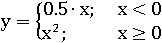
В этой формуле после y= возможны два варианта ее продолжения 0.5∙x и x2. Поэтому в ней содержатся сразу две такие формулы
y = 0.5∙x
y = x2
Значение кусочной функции следует вычислять по одной из этих двух формул. А по какой именно из них подскажут, указанные в формуле кусочной функции, эти условия:
x<0
x≥0
Если значение x будет меньше нуля, т.е. выполняется первое условие x<0, то вычислять значение функции следует по первому варианту формулы:
y = 0.5∙x
Если значение x будет больше нуля или равно ему, то выполняется второе условие x≥0, значит, вычислять значение кусочной функции нужно по второй формуле:
y = x2
Вычислим значение этой функции в точке x = −4. Для этого сначала определим, каким вариантом формулы нужно воспользоваться. Мысленно подставляем в условия вместо x число −4. Какое из условий верно для числа −4 ? Очевидно, что верно первое условие x<0, поскольку −4 меньше нуля:
x<0
−4<0
В строке с первым верным для x = −4 условием и находится вариант формулы, по которому надо вычислять значение кусочной функции:
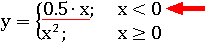
Подставим −4 вместо x в первую формулу y = 0.5∙x:
y = 0.5∙(−4) = −0.5∙4 = −2
Значит, значение кусочной функции в точке x = −4 равно −2.
Попробуем определить значение этой же кусочной функции в точке x = 3. На этот раз первое условие будет не верным, а второе – верным, потому что 3 больше нуля:
x≥0
3≥0
Следовательно, нужно выбрать второй вариант формулы y = x2:
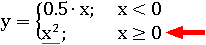
Тогда значение кусочной функции в точке x = 3 равно 9:
y = 32 = 9
Выходит, что все x, которые меньше нуля нужно подставлять в первую формулу; а все x, которые больше нуля или равны ему – во вторую. Например, значение этой функции в точке x = −1 следует вычислять по первому варианту формулы, потому что −1 меньше нуля:
y = 0.5∙(−1) = −0.5
Значит, значение функции в точке x = −1 равно −0.5.
Чтобы определить значение функции в точке x = 0, нужно применить второй вариант формулы, так как 0 равен нулю:
y = 02 = 0
Получается, что значение функции в точке x = 0 равно нулю.
Число −1.8 меньше нуля, следовательно, применяем первый вариант формулы, тогда значение функции в точке x = −1.8 будет равно −0.9:
y = 0.5∙(−1.8) = −0.9
Число 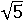 больше нуля, значит, вычисляем по второму варианту формулы, которая показывает, что значение функции в точке
больше нуля, значит, вычисляем по второму варианту формулы, которая показывает, что значение функции в точке 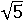 равно 5:
равно 5:
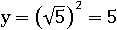
В первом условии этой функции сказано, что x может быть любым числом меньше нуля, а второе условие говорит, что x может быть любым числом равным нулю или больше нуля. Получается, что областью определения является всё множество действительных чисел – нет такого действительного числа, которое не подошло бы ни к одному из двух условий. Значением этой функции тоже может стать любое действительное число, следовательно, областью значений функции также является множество действительных чисел.
Кусочные функции могут включать в себя и больше двух вариантов формул и условий, но вычисляют значения этих функций по тому же принципу, просто выбирать нужно будет одну формулу не из двух, а из трех или четырех. Например, в следующей функции сразу три варианта формул:
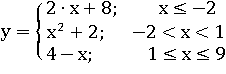
Значение такой функции определяют по одной из этих формул:
y = 2∙x+8
y = x2+2
y = 4−x
Первый вариант y = 2∙x+8 следует применять, для всех x, которые меньше числа −2 либо равны −2, т.е. для всех чисел из промежутка (−∞; −2]. Например, число −4.65 принадлежит промежутку (−∞; −2], тогда значение этой функции в точке x = −4.65 равно −1.3:
y = 2∙(−4.65)+8 = −9.3+8 = −1.3
Значение функции в точке x = −2 тоже нужно вычислять по первой формуле, поскольку только первое условие верно для числа −2:
y = 2∙(−2)+8 = −4+8 = 4
Для любого числа x, которое больше −2 и меньше 1, надо применять вторую формулу. Например, при x = 0.7 y равен 2.49, следовательно, значение функции в точке x = 0.7 равно 2.49:
y = 0.72+2 = 0.49+2 = 2.49
Ко всем x от 1 включительно до 9 включительно применяют третий вариант формулы y = 4−x. Так значение функции в точке x = 5.3 равно −1.3:
y = 4−5.3 = −1.3
Числа 1 и 9 подходят третьему условию 1≤x≤9, поэтому значение функции в точке x = 1 и x = 9 вычисляют тоже по третьей формуле:
y = 4−1 = 3
y = 4−9 = −5
Но ни одно число, которое больше 9-ти, не будет подходить ни в одно из трех условий, значит, значение функции в точках x, которые больше 9-ти, не существуют, следовательно, эти числа просто не входят в область определения, которая равна множеству чисел из промежутка (−∞; 9]. Область значений этой функции состоит из чисел, входящих в промежуток (−∞; 4], это значит, что значением функции может стать любое число, которое меньше четырех или равно четырем, но не больше четырех.