Обозначения y=f(x), D(f) и E(f)
Что значит запись y = f(x)
Подобно тому, как любое число можно обозначить переменной, любое выражение, содержащее x можно записать в таком виде:
f(x)
Читается «эф от икс».
А выражение, содержащее переменную a можно обозначить так:
f(a)
Например, f(x) может быть выражением x+2, тогда:
f(x) = x+2
Теперь вместо того, чтобы всякий раз писать x+2, можно написать просто f(x), поскольку уже заранее оговорено, чем следует считать f(x).
Если требуется определить значение выражения x+2 при x = 6, то нужно в формуле f(x) = x+2 все x поменять на 6 и вычислить:
f(6) = 6+2 = 8
Тогда не возникает нужды в длинной фразе «значение выражения x+2 при x = 6 равно 8», для этого, хватит и такой записи:
f(6) = 8
Произносится это так: «эф от шести равно восьми».
Возьмем такую функцию:
y = x+2
Ее областью определения и областью значений является множество всех действительных чисел. Формула этой функции тоже включает выражение, содержащее переменную x, значит можно заменить x+2 на f(x) и записать эту функцию уже в таком виде:
y = f(x)
Это позволяет делать многие записи более короткими и удобными. Теперь не обязательно при каждом упоминании функции y = x+2 писать или произносить всю ее формулу, которая может быть довольно большой, вполне достаточно указать один раз, что f(x) = x+2, а затем использовать формулу y = f(x).
Значение функции y = x+2 в точке 7 равно девяти:
y = 7+2 = 9
Чтобы сообщить, что значение функции в точке x = 7 равно девяти, можно просто сказать «эф от семи равно девяти»; в письменной форме это выглядит так:
f(7) = 9
Также легко можно указать значения этой функции при x = 8 и x = 9, как и при любых других значениях x из области определения:
f(8) = 10
f(9) = 11
Введем функцию, у которой область определения и значений – тоже множество действительных чисел:
y = 3∙x−5
Для обозначения функции можно использовать любую букву (не только f ). Еще функции часто называют буквами g и h. Если нужно работать с несколькими функциями сразу, то их следует обозначить разными буквами. Например, обозначим за g(x) выражение 3∙x−5 в функции y = 3∙x−5:
g(x) = 3∙x−5
Значение функции y = g(x) в точке 7 равно 16:
g(7) = 3∙x−5 = 3∙7−5 = 21−5 = 16
А значение функции y = f(x) в той же точке 7 было равно 9:
f(7) = x+2 = 7+2 = 9
Значит, сумма значений f(7) и g(7) равна 25:
f(7)+g(7) = 9+16 = 25
Когда нужно часто вычислять именно сумму значений двух разных функций, лучше сразу сложить x+2 и 3∙x−5, чтобы вывести такую формулу:
f(x)+g(x) = x+2+3∙x−5 = 4∙x−3
Тогда
f(x)+g(x) = 4∙x−3
Теперь нужно просто подставить вместо всех x нужное число 7 и получиться должно тоже 25, только быстрее:
f(7)+g(7) = 4∙x−3 = 4∙7−3 = 28−3 = 25
Так можно вычислить сумму f(x) и g(x) для любых x из области определения:
f(8)+g(8) = 4∙8−3 = 32−3 = 29
f(9.5)+g(9.5) = 4∙9.5−3 = 38−3 = 35
f(10)+g(10) = 4∙10−3 = 40−3 = 37
Если считать по отдельности f(x) и g(x) и потом складывать, то получатся точно такие же результаты:
f(9.5) = x+2 = 9.5+2 = 11.5
g(9.5) = 3∙x−5 = 3∙9.5−5 = 28.5−5 = 23.5
f(9.5)+g(9.5) = 11.5+23.5 = 35
f(10) = x+2 = 10+2 = 12
g(10) = 3∙x−5 = 3∙10−5 = 30−5 = 25
f(10)+g(10) = 12+25 = 37
Можно вывести и формулу произведения f(x) и g(x):
f(x)∙g(x) = (x+2)∙(3∙x−5)
f(x)∙g(x) = 3∙x2−5∙x+6∙x−10
Сложим −5∙x и 6∙x:
f(x)∙g(x) = 3∙x2+x−10
Тогда произведение значений функций y = f(x) и y = g(x) в точке x = 11 должно быть равно 364:
f(11)∙g(11) = 3∙x2+x−10 = 3∙112+11−10 =
3∙121+11−10 = 363+1 = 364
Проверим, правда ли произведение этих функций равно 364 при x = 11. Вычислим f(11) и g(11):
f(11) = x+2 = 11+2 = 13
g(11) = 3∙x−5 = 3∙11−5 = 33−5 = 28
Умножим 13 и 28:
f(11)∙g(11) = 13∙28 = 364
Получилось тоже 364 – всё верно.
Для того, чтобы задать функции y = f(x) и y = g(x) мы использовали такие формулы:
y = x+2
y = 3∙x−5
Но для удобства во многих случаях те же функции задают без использования зависимой переменной сразу такими формулами:
f(x) = x+2
g(x) = 3∙x−5
Такая форма записи позволяет избавиться от дополнительных пояснений о том, какую функцию из двух функций обозначили буквой f, а какую буквой g.
Довольно часто пользуются записью y = f(x), когда речь идет не о какой-то конкретной функции, а вообще об абстрактной функции. В этом случае имеют в виду, что просто есть некая зависимость значения переменной y от значения переменной x.
D(f) – область определенияи, E(f) – область значений
Из предыдущей статьи должно быть известно, что множество всех чисел, которых можно подставлять вместо x в формулу функции называется областью определения. Если подставить каждое число из области определения в формулу функции, то множество всех этих возможных значений функции будет называться областью значений.
Область определения функции принято обозначать буквой D, после которой в скобках указывают нужную функцию. Например, область определения функции y = f(x) можно обозначить так:
D(f)
Если требуется указать область определения функции y = g(x), то пишут букву g:
D(g)
Область значений функции y = f(x) обозначают буквой E с указанием функции в скобках:
E(f)
А область значений функции y = g(x) следует обозначать так:
E(g)
Как правило, в условиях задачи ничего не говорят про область определения и область значений функции. В таком случае под областью определения понимают множество всех допустимых значений независимой переменной, при которых формула функции имеет смысл; а областью значений функции следует считать множество чисел, состоящее из всех значений, которые сможет принять зависимая переменная.
Например, рассмотрим функцию, в описании которой явно область определения не указана:
y = 5∙x−9
Обозначим 5∙x−9 за f(x):
f(x) = 5∙x−9
Видно, что в эту функцию вместо x можно подставить совершенно любое действительное число: не произойдет таких недопустимых операций как деление на ноль или извлечение квадратного корня из отрицательного числа. Значит, ее область определения – множество всех действительных чисел, которое обозначается промежутком от минус бесконечности до плюс бесконечности:
D(f) = (−∞; +∞)
Исследуем область значений этой функции. Если вместо x подставить −2, то y будет равен −19, значит, числу −2 соответствует число −19:
y = f(−2) = 5∙(−2)−9 = −10−9 = −19
Если x = −1, то y = −14, значит, числу −1 соответствует число −14:
y = f(−1) = 5∙(−1)−9 = −5−9 = −14
И так далее:
y = f(0) = 5∙0−9 = 0−9 = −9
y = f(1) = 5∙1−9 = 5−9 = −4
y = f(2) = 5∙2−9 = 10−9 = 1
y = f(3) = 5∙3−9 = 15−9 = 6
y = f(3.1) = 5∙3.1−9 = 15.5−9 = 6.5
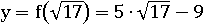
Составим таблицу, в которую включим все эти соответствия и некоторые другие.
| X | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| Y | -19 | -14 | -9 | -4 | 1 |
| X | 3 | 3.1 | 3.14 | 3.141 | 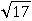 |
|---|---|---|---|---|---|
| Y | 6 | 6.5 | 6.7 | 6.705 | 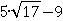 |
По таблице можно заметить, что при каждом увеличении x на единицу y будет всегда увеличиваться на 5; а при каждом уменьшении x на 1 y уменьшается на 5. Следовательно, y (вслед за x) может увеличиваться до бесконечности и уменьшаться до минус бесконечности, и при этом не будет пропускать ни одного действительного числа. Значит, значением этой функции может стать любое число, ее область значений – всё множество действительных чисел:
E(f ) = (−∞; +∞)
Теперь, когда нам уже известны все преимущества использования записи f(x), уже нет причин в постоянном употреблении переменной y, вместо нее можно применять запись f(x), потому что она тоже равна значению функции, как и y. Тогда зададим следующую функцию не формулой 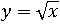 , а так:
, а так:
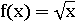
Квадратный корень можно извлечь из любого неотрицательного числа, значит, все положительные числа и ноль точно войдут в область определения функции 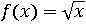 . Но операция извлечения квадратного корня из отрицательного числа не выполнима внутри множества действительных чисел, следовательно, отрицательных чисел в области определения этой функции нет – туда войдут только неотрицательные:
. Но операция извлечения квадратного корня из отрицательного числа не выполнима внутри множества действительных чисел, следовательно, отрицательных чисел в области определения этой функции нет – туда войдут только неотрицательные:
D(f ) = [0; +∞)
В результате извлечения квадратного корня из положительного числа может получиться только положительное число, а квадратный корень из нуля равен нулю. Значит, область значений функции 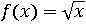 тоже состоит из всех положительных чисел и нуля:
тоже состоит из всех положительных чисел и нуля:
E(f ) = [0; +∞)
Теперь рассмотрим следующую функцию:
f(x) = x2
Очевидно, что в квадрат можно возвести совершенно любое действительное число, значит, область определения этой функции – множество всех действительных чисел:
D(f ) = (−∞; +∞)
Если в квадрат возвести действительное число, то получиться может уже только неотрицательное число; f(x) как раз и равен такому квадрату числа, значит, f(x) может быть только неотрицательным числом, следовательно, область значений этой функции можно приравнять к промежутку от нуля включительно до плюс бесконечности:
E(f ) = [0; +∞)
Случается, что в область определения не может входить только одно число из всех действительных, как в этой функции:
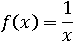
В функции 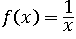 значение x может быть каким угодно кроме нуля. Деление на ноль – невыполнимая операция, выражение
значение x может быть каким угодно кроме нуля. Деление на ноль – невыполнимая операция, выражение 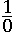 не имеет смысла. Чтобы исключить только ноль из области определения используем объединение двух промежутков:
не имеет смысла. Чтобы исключить только ноль из области определения используем объединение двух промежутков:
D(f ) = (−∞; 0)∪(0; +∞)
Значением функции 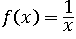 тоже может стать совершенно любое число кроме нуля – нет такого числа, на которое можно разделить единицу и получить ноль:
тоже может стать совершенно любое число кроме нуля – нет такого числа, на которое можно разделить единицу и получить ноль:
E(f ) = (−∞; 0)∪(0; +∞)
В любом случае если в формуле функции присутствует дробь, в знаменателе которой есть переменная, то обязательно нужно узнать при каком значении этой переменной знаменатель будет равен нулю – такие значения переменной не должны входить в область определения. Например, из области определения нужно исключить сразу два числа в этой функции:
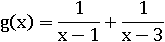
Переменная x может быть любым числом кроме 1 и 3. Приравняем область определения функции g(x) к объединению промежутков, в которое входят все действительные числа кроме 1 и 3:
D(g) = (−∞; 1)∪(1; 3)∪(3; +∞)
В область значений функции g(x) входят все действительные числа, в том числе ноль при x = 2:
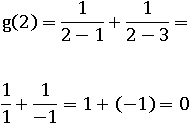
E(g) = (−∞; +∞)
Наличие в формуле функции дроби со знаменателем, содержащим переменную, не обязательно означает отсутствие каких-нибудь чисел в области определения. В следующей функции число 1 – наименьшее, которым может стать знаменатель, значит, знаменатель никогда не будет равным нулю:
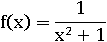
Действительно, число x 2 не может быть меньше нуля, следовательно, выражение x 2+1 не может быть меньше единицы, тогда значение выражения x 2+1 не равно нулю при всех действительных x, а область определения ничем не ограничена и равна множеству R:
D(f ) = (−∞; +∞)
Чем меньше знаменатель тем, больше значение этой функции. При x=0 знаменатель наименьший, а значит, и максимальное значение функции, равное единице, достигается при x = 0:
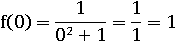
Чем больше знаменатель, тем ближе значение функции приближается к нулю, но оно никогда не сможет стать равным нулю:

Из всего этого можно заключить, что область значений этой функции – множество всех чисел от нуля не включительно до единицы включительно:
E(f ) = (0; 1]
Подобными методами можно найти область определения и область значений у значительной части школьных функций. Но всё же этого недостаточно, чтобы найти D(f ) и особенно E(f ) такой функции:
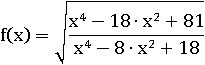
С более серьезными математическими инструментами, позволяющими это сделать, мы будем постепенно знакомиться по мере изучения всей оставшейся школьной программы и сможем определить, что D(f ) и E(f ) этой функции равны:
D(f ) = (−∞; +∞)
![Область значений E(f)=[0; (3√6)/2 ]](img2/f100.png)
Наименьшее значение 0 функция принимает при x=3 и при x=−3:
f(3)=0 f(−3)=0
Наибольшее значение функции 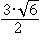 достигается при
достигается при 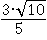 и при
и при 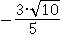 :
: