Основное свойство дроби

Приступим к изучению одной из самых простых и самоочевидных математических закономерностей, но пренебрежение которой приводит к самым печальным последствиям в дальнейшем.

Есть такая операция – деление, ее иногда обозначают двумя точками:

Но часто удобнее такая форма записи:

Обе формы записи совершенно равнозначны. Смысл одинаковый, только вместо двух точек – дробная черта. Делимое – это числитель, а делитель – это знаменатель:

А теперь приступим к самому главному

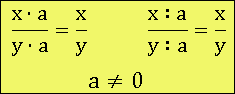
Это значит, что если взять какую-нибудь дробь, равную допустим двум:

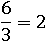
и умножить в ней 6 на 2 и 3 на 2, то получившаяся дробь будет также равна двум:

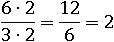
Основное свойство дроби оказалось верным: 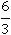равно двум и 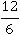– равно двум. Это свойство будет верным для любых дробей, например, одна вторая равна 0.5:

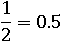
И если умножить на 5 числитель и знаменатель, то число 0.5 не изменится, потому что 5 деленое на 10 тоже равно 0.5:

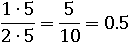
Возьмем дробь, значение которой равно четырем:

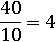
и в этот раз разделим числитель и знаменатель на одно и то же число, например на 5:

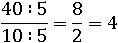
И даже если сам числитель или знаменатель будет дробью:

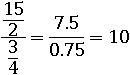
то домножение на 7 ничего не изменит:

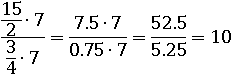
Значит это выражение:

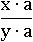
Можно упростить до такого выражения:

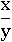
Умножение на a ничего не меняет - обе дроби равны при всех a не равных нулю (a≠0):

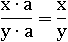
Такое упрощение называют сокращением. В таких случаях иногда просто зачеркивают два одинаковых множителя:

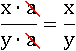
Из-за этого и возникает иллюзия, что в дроби можно свободно зачеркнуть два любых одинаковых числа. Тут-то и возникает одна из самых распространенных ошибок. Рекомендую посмотреть следующий пример, прекрасно иллюстрирующий эту ошибку. Возьмем число 2 в виде дроби:

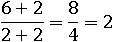
И зачеркнем в нем две одинаковые двойки, получится уже не число 2:

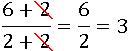
Потому что основное свойство дроби говорит, что можно только разделить или умножить на одно и то же число, а не отнять или прибавить. Эту дробь можно сократить только разделив на два числитель и знаменатель:

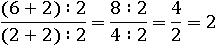
Но будет гораздо полезнее уметь сокращать другим способом: превратив числитель 6+2 в равное ему число (3+1)∙2, а знаменатель, равный четырем, можно заменить на число (1+1)∙2. Тогда в дроби появляется умножение числителя и знаменателя на два, а значит уже можно убрать обе двойки:

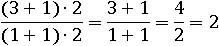
Этот способ сокращения дроби понадобится, когда уже не получится просто сложить 6 и 2, потому что там будут уже переменные.

Есть еще одна типичная ошибка. Конечно, в основном свойстве дроби не написано, что нужно умножать именно весь целиком числитель и знаменатель на любое число не равное нулю, но предполагается именно это. Поэтому следует всегда понимать: умножать или делить числитель и знаменатель надо сразу весь. Возьмем дробь равную пяти:

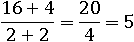
И домножим на два следующим образом:

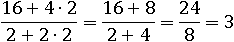
Почему же получилось совсем другое число? Потому что умножать надо было весь числитель и знаменатель и все сразу встанет на свои места:

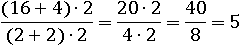
Разумеется, то же относится и к делению. Попробуем в этой же дроби разделить на 2 не все число 20, а только 4, и только двойку в знаменателе:

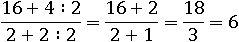
Опять получилось не 5. А теперь разделим правильно:

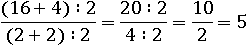
Или так:

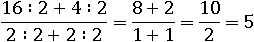
Теперь все сходится.

Основное свойство дроби абсолютно также работает и в случае, когда в дроби есть переменные, т.к. переменные – это те же самые числа, только не конкретные, а вообще какие-то абстрактные числа.

Возьмем, например, такую дробь:

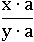
В случае если число x=9, y=3, a=4, то эта дробь будет равна трем:

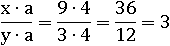
Но свойство дроби говорит нам, что данная дробь абсолютно равносильна той же только без числа a, при условии, что a не равно нулю:

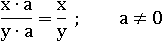
Проверим это, подставив вместо переменных те же числа:

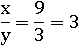
Получилось такое же значение как и у изначальной дроби. Можно проверить равносильность этих дробей, подставив вместо переменных x, y и a совершенно любые три числа (только a≠0) – результат будет в обеих дробях совершенно одинаковым.

Попробуем упростить следующее выражение:

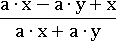
Допустим, что x=7, y=3, a=5, тогда дробь будет иметь такое значение:

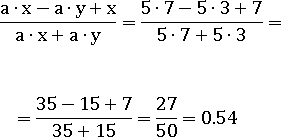
Теперь разделим весь числитель и весь знаменатель на число a≠0:

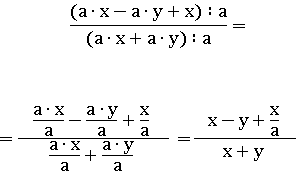
Выражение упростилось – один раз разделить на a проще чем четыре раза умножать на a. Проверим, подставив те же числа:

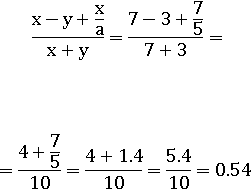
Так мы получили выражение равносильное изначальному:

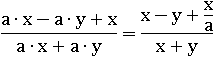
Не только делением можно упростить выражение, но еще и умножением числителя и знаменателя на одно и тоже число, как в следующей дроби:

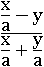
Пусть x=4, y=8, a=2, тогда:

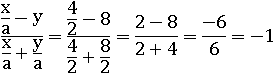
А теперь домножим на a:

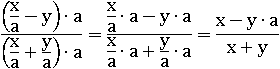
И опять подставим эти же числа:

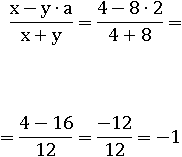
Основное свойство дроби оказывается часто полезным и при выполнении элементарных арифметических операций. Допустим, требуется разделить 143 на 5:

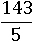
Не будем сразу делить в столбик, а подумаем о том, как можно упростить вычисления. Попробуем домножить на 2:

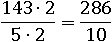
А вот делить на 10 уже гораздо проще – достаточно перенести запятую на одну цифру влево:

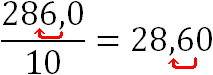
В результате вместо более сложного деления на 5 мы просто умножили на 2.

Или еще возможен такой случай:

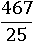
Тут можно домножить на 4, чтобы в знаменателе получить удобное число 100, на которое делить очень просто:

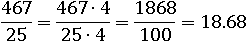
Можно использовать не только домножение, но и деление числителя и знаменателя:

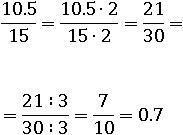
Основное свойство дроби на этом не заканчивается, теперь оно будет применяться везде, где только будет дробь, то есть везде.

© Кирилл Морковкин & Машка Кулибякина